Digitale Werkzeuge in der Schule/Basiswissen Analysis/Optimierungsprobleme: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 113: Zeile 113:
{{Lösung versteckt | 1=
{{Lösung versteckt | 1=
Die Definitionsmenge für die Zielfunktion <math>V(a)</math> ergibt sich aus der Bedingung für die Länge (<math>b</math>).
Die Definitionsmenge für die Zielfunktion <math>V(a)</math> ergibt sich aus der Bedingung für die Länge (<math>b</math>).
Die Länge muss zum einen größer gleich <math>0 cm</math> und zum anderen kleiner gleich <math>200 cm</math> sein. Also gelten die folgenden zwei Ungleichungen, die du einfach nach <math>a</math> auflösen kannst.  
Die Länge muss zum einen größer gleich <math>0</math> und zum anderen kleiner gleich <math>200</math> sein. Also gelten die folgenden zwei Ungleichungen, die du einfach nach a auflösen kannst.  
<math>0</math><math>\leq</math><math>360-4*a</math>  und
<math>0</math><math>\leq</math><math>360-4*a</math>  und
<math>200</math><math>\geq</math><math>360-4*a</math>.
<math>200</math><math>\geq</math><math>360-4*a</math>.
Zeile 122: Zeile 122:
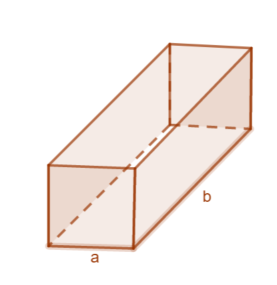
<math>V(a,b) = a * a * b = a^2 *b</math>.
<math>V(a,b) = a * a * b = a^2 *b</math>.


'''Nebenbedingung aufstellen''': Durch die zweite Bedingung können wir die folgende Gleichung aufstellen:
'''Nebenbedingung aufstellen''': Durch die zweite Bedingung können wir die folgende Gleichung aufstellen.
<math> b + 4*a = 360</math>.  
<math> b + 4*a = 360</math>.  
Die Gleichung stellen wir nach <math>b</math> um und erhalten:
Die Gleichung stellen wir nach <math>b</math> um und erhalten:
<math>b = 360 - 4*a</math>.
<math>b = 360 - 4*a</math>.
Nun können wir b in die Zielfunktion <math>V(a,b)</math> einsetzen, welche dann noch von der Variable <math>a</math> abhängt. Wir schreiben dann für die Funktion <math>V(a)</math> und erhalten <math>V(a) = -4a^3 + 360 a^2</math>.
Nun können wir <math>b</math> in die Zielfunktion <math>V(a,b)</math> einsetzen, welche dann durch noch von der Variable <math>a</math> abhängt. Wir schreiben dann für die Funktion <math>V(a)</math> und erhalten <math>V(a) = -4*a^3 + 360 a^2</math>.


'''Definitionsmenge angeben''': Wir wollen nun eine Definitionsmenge für die Funktion <math>V(a)</math> angeben. Diese erhalten wir, indem wir uns die Bedingung für die Länge (<math>b</math>) anschauen.  
'''Definitionsmenge angeben''': Wir wollen nun eine Definitionsmenge für die Funktion <math>V(a)</math> angeben. Diese erhalten wir, indem wir uns die Bedingung für die Länge (<math>b</math>) anschauen.  
Offensichtlich muss die Länge größer gleich <math>0 cm</math> sein. Es gilt also:
Offensichtlich muss die Länge größer gleich <math>0</math> sein. Es gilt also:
<math>360 - 4*a \geq 0</math>.  
<math>360 - 4*a \geq 0</math>.  
Durch das Umstellen nach <math>a</math> folgt:<math>a \leq 90</math>.
Durch das Umstellen nach <math>a</math> folgt:<math>a \leq 90</math>.
Außerdem muss die Länger kleiner gleich <math>200 cm </math> sein. Es gilt also:
Außerdem muss die Länger kleiner gleich <math>200 cm </math> sein. Es gilt also:
<math>360 - 4*a \leq 200</math>.  
<<math>360 - 4*a \leq 200</math>.  
Durch das Umstellen nach <math>a</math> folgt: <math>a \geq 40</math>.
Durch das Umstellen nach <math>a</math> folgt: <math>a \geq 40</math>.
Insgesamt ergibt das also <math>40 \leq a \leq 90</math>.  
Insgesamt ergibt das also <math>40 \leq a \leq 90</math>.  


Nun sollen die '''Extremstellen''' von <math>V(a)</math>'''bestimmt werden'''.
Nun sollen die Extremstellen von <math>V(a)</math>bestimmt werden.


<math>V'(a) = -12a^2 + 720a</math>
<math>V'(a) = -12a^2 + 720a</math>
Zeile 144: Zeile 144:


Notw. Bedingung: <math>V'(a) = 0 </math>.
Notw. Bedingung: <math>V'(a) = 0 </math>.
<math> -12a^2 + 720a = 0 </math> (Klammere das <math>a</math> aus und wende den Satz vom Nullprodukt an. Alternativ kannst du auch die pq-Formel anwenden)
<math> -12a^2 + 720a = 0 </math> (Klammere das <math>a</math> aus und wende den Satz vom Nullprodukt an. Alternativ kannst du auch die pq-Formel anwenden)
<math> (-12a + 720)a = 0 </math>
<math> (-12a + 720)a = 0 </math>
<math>-> a=0 </math> oder <math> -12a + 720 = 0 </math>.
<math>-> a=0 </math> oder <math> -12a + 720 = 0 </math>.
Da <math>a \geq 40</math> muss <math> -12a + 720 = 0 </math> gelten, also <math> a = 60 </math>.
Da <math>a \geq 40</math> muss <math> -12a + 720 = 0 </math> gelten, also <math> a = 60 </math>.
Durch das Einsetzen von <math> a = 60 </math> in <math>V''(a)</math> folgt, dass <math>V(a)</math> an dieser Stelle einen Hochpunkt besitzt.
Durch das Einsetzen von <math> a = 60 </math> in <math>V''(a)</math> folgt, dass <math>V(a)</math> an dieser Stelle einen Hochpunkt besitzt.
Breite und Höhe sind also <math>60 cm</math>.
Breite und Höhe sind also <math>60 cm</math>.
Die Länge ergibt sich durch das einsetzen von <math> a = 60</math> in <math> b = 360 - 4*a</math>.
Die Länge ergibt sich durch das einsetzen von <math> a = 60</math> in <math> b = 360 - 4*a</math>.

Version vom 18. Mai 2020, 09:47 Uhr

Info

In diesem Kapitel kannst du etwas zum Thema Optimierungsprobleme lernen.

In Aufgaben, die orange gefärbt sind, kannst du Gelerntes wiederholen und vertiefen.

Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.

Und Aufgaben mit grüner Hinterlegung sind Knobelaufgaben.

Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.

In diesem Kapitel erklären wir dir zunächst, was Optimierungsprobleme sind. Dabei werden wir wichtige Begriffe wiederholen.

Anschließend kannst du selbstständig Aufgaben bearbeiten.

Viel Erfolg!


Einführung: Optimierungsprobleme

Was sind Optimierungsprobleme?

Optimierungsprobleme , oder auch Extremwertprobleme, beschreiben eine Aufgabenform, bei der nach dem optimalen Wert einer Funktion gefragt wird. Dieser optimale Wert ist oftmals ein Extremwert, also ein Maximum oder ein Minimum.

Die Berechnung erfolgt dabei im Sachzusammenhang, es wird also beispielsweise nach dem minimalen Volumen einer Schachtel gefragt, die man mit einem Blatt Papier falten kann, oder nach dem maximalen Flächeninhalt eines Grundstücks, das man mit einer bestimmten Meterzahl an Zaunteilen einzäunen kann.

Die Funktion, deren Extremwert es zu bestimmen gilt, muss also noch ermittelt werden.

Vorgehen beim Lösen von Optimierungsproblemen

So löst du Optimierungsprobleme

Bei Optimierungsproblemen geht es stets darum, dass eine bestimmte Größe optimiert werden soll. So wird z. B. eine optimale Verpackung für Reis oder die optimale Anzahl an Zahnpasten gesucht, die in einen Karton passen - es geht also um eine Anwendungssituation. Das Ergebnis eines Optimierungsproblems ist daher auch meist kein exakter Wert sondern ein Näherungswert. Dieser muss natürlich sinnvoll gewählt sein.

Zur Lösung eines Optimierungsproblems muss man zunächst die Aufgabe genau lesen und verstehen. Hierbei kann man sich die folgenden Fragen stellen: Worum geht es? Welche Größen kommen vor und wie hängen sie zusammen? Welche Größe soll nun optimiert, also maximiert oder minimiert werden?

Der optimale Wert bedeutet mathematisch, den Extremwert einer Funktion zu bestimmen. Du musst also das Optimierungsproblem als Funktion ausdrücken und dabei die anderen Größen miteinbeziehen. Mit dieser Funktion kannst du dann den optimalen Wert bestimmen.


Aufgabe 1: Beispiel


Ein Sportplatz mit einer 400-m-Laufbahn soll so angelegt werden, dass das Fußballfeld möglichst groß ist. Die seitlichen Kurven des Sportplatzes sollen Halbkreise sein.

a) Für welche Länge und für weiche Breite wird das Fußballfeld im Inneren des Sportplatzes maximal?

b) Wie groß ist das Fußballfeld?

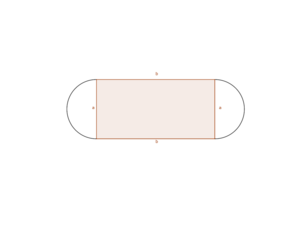
Gegeben ist die Länge der Laufbahn um den Sportplatz herum, also der Umfang des Sportplatzes. Maximiert werden soll die Größe des Fussballfeldes, also der rechteckige Flächeninhalt innerhalb des Sportplatzes.

Skizze .png

Die Formel zum Flächeninhalt ist . Über die Größen selbst weißt du ebenfalls etwas durch den Umfang: . Stelle die Formel für den Umfang nun nach um und erhalte:

Setze nun deine Formel für in den Flächeninhalt ein. So erhälst du die folgende Zielfunktion:

Für diese Funktion kann nur zwischen und liegen, also

Nun musst du den optimalen Wert berechnen. Gesucht ist hier das Maximum. Bilde dazu die Ableitungen:

Mit der notwendigen Bedingung erhälst du dann . Mit der hinreichenden Bedingung folgt , somit erfüllt alle Bedingungen.

Berechne nun und den Flächeninhalt:

  1. und

a) Der Flächeninhalt des Fussballfeldes wird für eine Breite von und eine Höhe von maximal.

b) Der Flächeninhalt wird auf maximiert.



Aufgabe 2: Das optimale Paket

Eine Kartonfabrik stellt quaderförmige Pakete mit quadratischen Seitenflächen () her. Damit die Pakete nicht zu unhandlich werden, sollen noch zwei Bedingungen erfüllt sein:

  • Die Länge () soll nicht größer als sein.
  • Länge () plus Umfang einer quadratischen Seitenfläche soll groß sein.
    300

a) Ermittle die Abmessungen des Pakets mit dem größten Volumen.

b) Gebe das maximale Volumen an.

Rechne Höhe () Breite () Länge (), um das Volumen eines Quaders (Paketes) zu ermitteln.

Nutze die zweite Bedingung, stelle eine Gleichung auf und stelle diese nach um.

Zweite Bedingung: Länge () plus Umfang einer quadratischen Seitenfläche soll groß sein. Den Umfang einer quadratischen Seitenfläche erhältst du, indem du rechnest.

Die Definitionsmenge für die Zielfunktion ergibt sich aus der Bedingung für die Länge (). Die Länge muss zum einen größer gleich und zum anderen kleiner gleich sein. Also gelten die folgenden zwei Ungleichungen, die du einfach nach a auflösen kannst. und

.

Zielfunktion aufstellen: Um das Volumen des Paktes zu errechnen, verwenden wir die folgende Funktion, die von den Variablen und abgängig ist: .

Nebenbedingung aufstellen: Durch die zweite Bedingung können wir die folgende Gleichung aufstellen. . Die Gleichung stellen wir nach um und erhalten: . Nun können wir in die Zielfunktion einsetzen, welche dann durch noch von der Variable abhängt. Wir schreiben dann für die Funktion und erhalten .

Definitionsmenge angeben: Wir wollen nun eine Definitionsmenge für die Funktion angeben. Diese erhalten wir, indem wir uns die Bedingung für die Länge () anschauen. Offensichtlich muss die Länge größer gleich sein. Es gilt also: . Durch das Umstellen nach folgt:. Außerdem muss die Länger kleiner gleich sein. Es gilt also: <. Durch das Umstellen nach folgt: . Insgesamt ergibt das also .

Nun sollen die Extremstellen von bestimmt werden.

.

Notw. Bedingung: .

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://en.wikipedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle -12a^{2}+720a=0} (Klammere das aus und wende den Satz vom Nullprodukt an. Alternativ kannst du auch die pq-Formel anwenden)

oder . Da muss gelten, also .

Durch das Einsetzen von in folgt, dass an dieser Stelle einen Hochpunkt besitzt.

Breite und Höhe sind also . Die Länge ergibt sich durch das einsetzen von in . .

Das Volumen bestimmen: Wir berechnen nun das Volumen des optimalen Paketes, indem wir berechnen.

Das maximale Volumen beträgt also .


Aufgabe 3: Die optimale Pommestüte

Leon möchte aus einem kreisförmigen Stück Papier mit dem Radius eine Pommestüte formen.

Dazu schneidet er den Kreis längs eines Radius ein. Nun versucht Leon die Pommestüte so zu formen, sodass das Volumen der Pommestüte maximal ist, damit auch möglichst viele Pommes hineinpassen.

Was ist das maximale Volumen der Pommestüte?
Gerader Kreiskegel.svg
Beachte, dass der Radius des Stücks Papier der Mantellinie des Kegels entspricht.
Das Volumen der Pommestüte errechnet man mit der Formel .
Mit Hilfe vom Satz des Pythagoras kannst du Fehler beim Parsen (Konvertierungsfehler. Der Server („https://en.wikipedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle s^{2}} bestimmen. Durch geeignetes Umstellen nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r^2} erhältst du schließlich eine geeignete Nebenbedingung.

Leon möchte aus einem kreisförmigen Stück Papier eine Pommestüte formen, in der möglichst viele Pommes hineinpassen. Zu optimieren ist also das Volumen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V(r,h)=\frac{1}{3} \cdot\pi\cdot r^2 h } der Pommestüte.

Rollt Leon das Stück Papier nicht, so ist ist das Volumen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V = 0} . Rollte Leon das Stück Papier ganz zusammen, so ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle s = h = 10} .

Gegeben ist die Mantellinie mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle s=10 } der Pommestüte. Außerdem ist das Volumen der Pommestüte von den Variablen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r } (Radius) und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h } (Höhe) abhängig. Mit dem Satz des Pythagoras ergibt sich Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r^2 + h^2 = 10^2 } . Stelle diese Gleichung nun nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r } um und erhalte Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r^2 = 100 - h^2 } .

Setze diesen Ausdruck nun für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r^2 } in die Formel für das Volumen ein. Du erhälst folgende Zielfunktion: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V(h)= \frac{1}{3} \pi (100-h^2)h = -\frac{1}{3} \pi h^3 + \frac{100}{3} \pi h} .

Für diese Funktion kann Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h } nur zwischen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0 } und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 10 } liegen, also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0<h<10 } .

Da es sich um eine Anwendungssituation handelt, reicht ein guter Näherungswert.

Die Ableitungsfunktion lautet Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V'(h)=- \pi*h^2 + \frac{100}{3} * \pi} .

Das maximale Volumen der Pommestüte beträgt ca. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 403cm^3}




Globales Extremum und Randextremum

Merke

Der größte Funktionswert unter allen Funktionswerten in der Definitionsmenge heißt globales Maximum. Der kleinste Funktionswert unter allen Funktionswerten in der Definitionsmenge heißt globales Minimum.

Ein globales Extremum an einer Randstelle der Definitionsmenge heißt Randextremum.
Übung



Aufgabe 4

Gegeben ist der Graph einer Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)=(x-3)^2+2,5} im Intervall Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle [0,3]} . Ein achsenparalleles Rechteck wird so gelegt, dass ein Eckpunkt der Koordinatenursprung ist und der gegenüberliegende Eckpunkt auf dem Graphen von f liegt.

Welches der möglichen Rechtecke hat den größten Flächeninhalt?
Aufgabe Ranextrema beachten.png

Mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x,y} in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle cm} berechnen wir den Flächeninhalt mit der Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A(x,y)=x*y} .

Die Nebenbedingung ist die angegebene Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)=f(x)=(x-3)^2+2,5} .

Setzt man nun die Nebenbedingung in die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A(x,y)} ein, so erhalten wir Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A(x)=x^3-6x^2+11x} . Die Funktion heißt nun Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A(x)} , da sie nur noch von der Unbekannte Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} abhängt.

Nun lässt sich mit Hilfe der notwendigen Bedingung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A'(x)=0} und der hinreichenden Bedingung für Hochpunkte Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A''(x) < 0 } die Stelle des lokalen Hochpunktes bestimmen. Anschließend setzen wir Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} in die Ausgangsfunktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A(x)} ein und erhalten nun den lokalen Hochpunkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle HP(1,59|7,14)} .

Zuletzt prüfen wir noch die Randpunkte.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A(0)=0} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A(3)=7,5} .

Damit liegt der globale Hochpunkt an der Stelle Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x=3} .


Der Flächeninhalt ist also am größten, wenn der zweite Eckpunkt des achsenparallelen Rechteckes an die Stelle Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x=3} gelegt wird. Der Flächeninhalt beträgt dann Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 7,5cm^2}

Optimierungsprobleme & Funktionenscharen

Berechnung von Extremwerten im Fall einer Funktionenschar

In bestimmten Fällen kann es vorkommen, dass die erhaltene Funktion nicht nur von einer Variable Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} abhängt, sondern außerdem von einem Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a} .

In diesem Fall ändert sich die Vorgehensweise bei der Berechnung des Extremwertes zwar nicht, allerdings ist das erhaltene Ergebnis dann abhängig von a.


Aufgabe 5 ⭐

Gegeben ist die Funktionenschar Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f_t(x)=x^2-4x-t^2-2t} .

Für welchen Wert von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t} liegt der Tiefpunkt der Funktionenschar am höchsten?


Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion.

Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t} .

Ableiten der Funktion ergibt:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x)=2x-4} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f''(x)= 2}


Für ein Minimum muss gelten: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x)=0} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f''(x)>0} .

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x)=0}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <=> 2x-4=0 }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <=> 2x=4}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <=> x=2}


Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f''(2) = 2 > 0 =>} Minimum

Setze nun Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x=2} in ein, um den Funktionswert am Minimum zu bestimmen:


Bezeichnen wir den Funktionswert am Tiefpunkt mit einer neuen Gleichung , so ergibt sich also:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(t)=-4-t^2-2t} .
Gesucht ist das Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t} , für das der Funktionswert maximal ist, also das Maximum der Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(t)} .
Prüfe die hinreichende Bedingung: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g'(t)=0} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g''(t)<0} .


Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion.

Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t} :

Ableiten der Funktion ergibt:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x)=2x-4} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f''(x)= 2}


Für ein Minimum muss gelten: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x)=0} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f''(x)>0} .

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x)=0}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <=> 2x-4=0 }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <=> 2x=4}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <=> x=2}


Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f''(2) = 2 > 0 =>} Minimum

Setze nun Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x=2} in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} ein, um den Funktionswert am Minimum zu bestimmen:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(2)=2^2-4*2-t^2-2t}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <=> f(2)=4-8-t^2-2t}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <=> f(2)=-4-t^2-2t}


Bezeichnen wir den Funktionswert am Tiefpunkt mit einer neuen Gleichung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} , so ergibt sich also:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(t)=-4-t^2-2t} .


Gesucht ist das Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t} , für das der Funktionswert maximal ist, also das Maximum der Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(t)} .

Bilde zunächst wieder die Ableitungen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g'(t)} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g''(t)} :

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g'(t)=-2t-2}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g''(t)=-2}

Bei einem Maximum muss gelten: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g'(t)=0} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g''(t)<0} .

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g'(t)=0}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <=>-2t-2=0}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <=>-2t=2}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <=>t=-1}


Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g''(-1)=-2<0 =>} Maximum

Der Funktionswert des Tiefpunktes ist also für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t=-1} maximal.
Abgerufen von „https://projektwiki.idea-sketch.com/index.php?title=Digitale_Werkzeuge_in_der_Schule/Basiswissen_Analysis/Optimierungsprobleme&oldid=21894“