Benutzer:Vivien WWU-6/TestseiteAufgaben: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(88 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
=== Monotonie ===
===Monotonie===
{{Box | Merksatz |  
{{Box | Merksatz |  


Das '''Monotonieverhalten''' einer Funktion
Das '''Monotonieverhalten''' einer Funktion


…beschreibt den Verlauf des Graphen einer Funktion. Sie gibt an, ob eine Funktion fällt, steigt oder konstant ist.
…beschreibt den Verlauf des Graphen einer Funktion. Die Montonie gibt an, ob eine Funktion fällt, steigt oder konstant ist.




Zeile 21: Zeile 21:




Tipp: Du kannst leicht mithilfe der ersten Ableitung überprüfen, ob die Steigung positiv oder negativ ist!
 
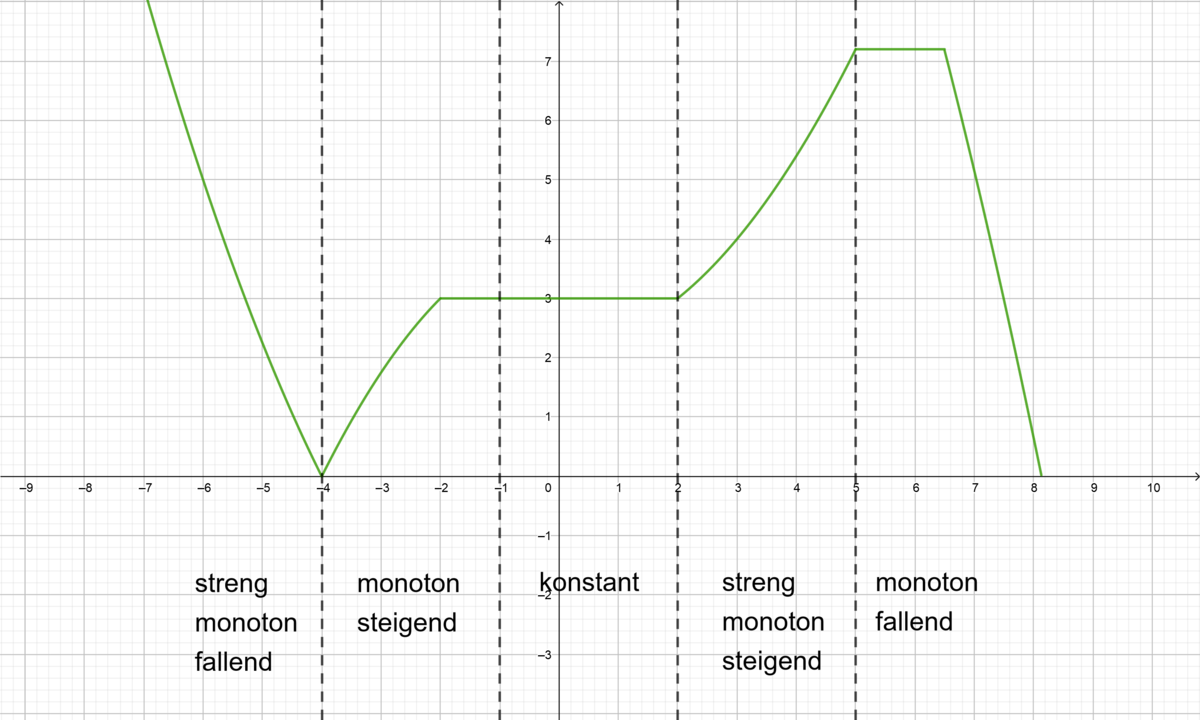
[[Datei:MonotonieAbbildung.png|links|1200x1200px]]


  | Merke}}
  | Merke}}


{{Box | Aufgabe 1 | Ordne den Funktionen den richtigen Begriff zu | Arbeitsmethode}}
{{Box | Aufgabe 1 |
{{LearningApp|width:100%|height:500px|app=p7pny09y220}}
{{LearningApp|width:100%|height:500px|app=p7pny09y220}} | Arbeitsmethode}}


Exponentialfunktion, cosinus/sinus auf Intervallen


{{Box| So berechnest du das Monotonieverhalten einer Funktion|
{{Box| So berechnest du das Monotonieverhalten einer Funktion|
Zeile 47: Zeile 47:
{{Box| Beispiel: Monotonieverhalten für <math>g(x)=x^2</math> bestimmen |  
{{Box| Beispiel: Monotonieverhalten für <math>g(x)=x^2</math> bestimmen |  
Zuerst berechnen wir die Ableitung <math>g'(x)=2x</math>. Anschließend berechnen wir die Nullstellen der Ableitung (<math>g'(x)=0</math>) und erhalten durch Umformungen als Nullstelle <math>x=0</math>.
Zuerst berechnen wir die Ableitung <math>g'(x)=2x</math>. Anschließend berechnen wir die Nullstellen der Ableitung (<math>g'(x)=0</math>) und erhalten durch Umformungen als Nullstelle <math>x=0</math>.
Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten <math>(-\infty,0)</math> und <math>(0,+\infty)</math>. Darauffolgend stellen wir eine Monotonietabelle auf und berechnen die Vorzeichen für die Intervalle:  
Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten <math>(-\infty,0)</math> und <math>(0,+\infty)</math>. Darauffolgend stellen wir eine Monotonietabelle auf und berechnen die Vorzeichen für die Intervalle: | Beispiel}}


| Beispiel}}
{| class="wikitable center"
{| class="wikitable center"
|-
|-
Zeile 62: Zeile 61:
|<math> > 0</math>
|<math> > 0</math>
|-
|-
|<math> G_{f} </math>
|Graph von f
|<math> \searrow </math>
|<math> \searrow </math>
|'''Tiefpunkt'''
|'''Tiefpunkt'''
Zeile 69: Zeile 68:


Aus dem Ergebnis können wir schließen, dass die Funktion für <math>(-\infty,0)</math> streng monoton fallend und für <math>(0,+\infty)</math> streng monoton steigend ist.  
Aus dem Ergebnis können wir schließen, dass die Funktion für <math>(-\infty,0)</math> streng monoton fallend und für <math>(0,+\infty)</math> streng monoton steigend ist.  
{{Box | Aufgabe 2 |
a) Auf dem Bild siehst du den Graphen einer Ableitungsfunktion <math>f'(x)</math>. Welche Aussagen kannst du über das Monotonieverhalten von <math>f(x)</math> machen?
[[Datei:Graph der Funktion f'(x).jpg|links|alternativtext=|544x544px]]
{{Lösung versteckt|1=Erinnere dich daran, wie du bei der Berechnung des Monotonieverhaltens vorgehst. Welche Aussagen zum Monotonieverhalten liefert dir <math>f'(x)=0</math>? |2=Tipp 1|3=Schließen}}
{{Lösung versteckt|1=Die Nullstellen von <math>f'(x)</math> definieren die verschiedenen Intervalle, in denen das Monotonieverhalten von <math>f</math> verschieden ist. Nun kannst du betrachten, auf welchen Intervallen <math>f'(x)</math> <math><0</math> bzw. <math>>0</math> ist. Welche Aussagen kannst du damit über das Monotonieverhalten von <math>f(x)</math> machen? |2=Tipp 2|3=Schließen}}
{{Lösung versteckt|1= Die Nullstellen von <math>f'(x)</math> sind <math>x_1=-3, x_2=-2</math> und <math>x_3=-1</math>.
Damit sind die zu betrachtenden Intervalle <math>(-\infty, -3)</math>, <math>(-3, -2)</math>, <math>(-2, -1)</math> und <math>(-1, +\infty)</math>. Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob <math>f'(x)</math> an diesen <math><0</math> oder <math>>0</math> ist.
Für <math>(-\infty, -3)</math> ist <math>f'(x)<0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton fallend.
Für <math>(-3, -2)</math> ist <math>f'(x)>0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton steigend. 
Für <math>(-2, -1)</math> ist <math>f'(x)<0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton fallend.
Für <math>(-1, +\infty)</math> ist <math>f'(x)>0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton steigend. |2=Lösung|3=Schließen}}
b) Zeichne nun mithilfe deiner Ergebnisse aus a) den Funktionsgraphen <math>f(x)</math> mithilfe deiner Kenntnisse über sein Monotonieverhalten in dein Heft.
{{Lösung versteckt|1=Dein Graph könnte in etwa so aussehen:
[[Datei:Graph f(x).jpg|links|544x544px]]
Möglich, weitere Lösungen für die Zeichnung des Graphen sind unter anderem Verschiebungen in Richtung der Ordinate, also nach unten und oben oder auch Streckungen bzw. Stauchungen. |2=Lösung|3=Schließen}} | Arbeitsmethode}}
{{Box | Aufgabe 3 |
a) Nach einem starken Regenschauer in Münster steigt der Wasserspiegel im Aasee an. Die Funktion <math>f(x)=\frac{1}{4}x^{3} -\frac{25}{2}x^{2} +144x</math> beschreibt die Zuflussgeschwindkeit in den ersten 72 Stunden. Wann fließt innerhalb dieser Zeit Wasser zu und wann Wasser ab?
b)
| Arbeitsmethode}}
Für Aufgabe 2a) Monotonietabelle
{| class="wikitable center"
|-
!
!<math> -\infty < x < 7,4 </math>
!<math> x = 7,4 </math>
!<math> 7,4 < x < 25,92 </math>
!<math> x = 25,92 </math>
!<math> 25,92 < x < \infty </math>
|-
|<math> g'(x) </math>
|<math> > 0 </math>
|<math> = 0 </math>
|<math> < 0</math>
|<math> = 0</math>
|<math> > 0</math>
|-
|Graph von <math>g</math>
|<math> \nearrow </math>
|'''Hochpunkt'''
|<math> \searrow </math>
|'''Tiefpunkt'''
|<math> \nearrow </math>
|}
Für 2b)
{| class="wikitable center"
|-
!
!<math> -\infty < x < -\frac{\sqrt{15}}{5}a </math>
!<math> f'\Big(-\frac{\sqrt{15}}{5}a \Big) </math>
!<math> -\frac{\sqrt{15}}{5}a < x < 0 </math>
!<math> f'\Big(0\Big) </math>
!<math> 0 < x < \frac{\sqrt{15}}{5}a </math>
!<math> f'\Big(\frac{\sqrt{15}}{5}a \Big) </math>
!<math> \frac{\sqrt{15}}{5}a < x < \infty</math>
|-
|<math> f'(x) </math>
|<math> < 0 </math>
|<math> = 0 </math>
|<math> > 0</math>
|<math> = 0</math>
|<math> < 0</math>
|<math> = 0 </math>
|<math> > 0</math>
|-
|<math> Graph  von  f </math>
|<math> \searrow </math>
|'''TP'''
|<math> \nearrow </math>
|'''HP'''
|<math> \searrow </math>
|'''TP'''
|<math> \nearrow </math>
|}
{| class="wikitable center"
|-
!
!<math> x=0 </math>
!<math> 0 < x < \frac{\sqrt{15}}{5}a </math>
!<math> x=\frac{\sqrt{15}}{5}a </math>
!<math> \frac{\sqrt{15}}{5}a < x  \leq \ 4</math>
|-
|<math> f_a'(x) </math>
|<math> = 0</math>
|<math> < 0</math>
|<math> = 0 </math>
|<math> > 0</math>
|-
| Graph von <math>f_a</math>
|'''HP'''
|<math> \searrow </math>
|'''TP'''
|<math> \nearrow </math>
|}




{{Box | Aufgabe 2 | Berechne das Monotonieverhalten folgender Funktionen | Arbeitsmethode}}


{| class="wikitable center"
{| class="wikitable center"
Zeile 101: Zeile 354:
!
!
!<math> -\infty < x < 0 </math>
!<math> -\infty < x < 0 </math>
!<math> f'(0) </math>
!<math> x=0 </math>
!<math> 0 < x < \infty </math>
!<math> 0 < x < \infty </math>
|-
|-
Zeile 109: Zeile 362:
|<math> > 0</math>
|<math> > 0</math>
|-
|-
|<math> G_{f} </math>
|Graph von <math> f </math>
|<math> \searrow </math>
|<math> \searrow </math>
|'''Tiefpunkt'''
|'''Tiefpunkt'''
|<math> \nearrow </math>
|<math> \nearrow </math>
|}
|}

Aktuelle Version vom 18. Mai 2020, 10:09 Uhr

Monotonie

Merksatz


Das Monotonieverhalten einer Funktion

…beschreibt den Verlauf des Graphen einer Funktion. Die Montonie gibt an, ob eine Funktion fällt, steigt oder konstant ist.


Sei eine Funktion und

-      Falls auf einem Intervall gilt, so ist die Funktion streng monoton steigend

-      Falls auf einem Intervall gilt, so ist die Funktion monoton steigend


-      Falls auf einem Intervall gilt, so ist die Funktion streng monoton fallend

-      Falls auf einem Intervall gilt, so ist die Funktion monoton fallend


MonotonieAbbildung.png


Aufgabe 1



So berechnest du das Monotonieverhalten einer Funktion


1. Erste Ableitung berechnen

2. Nullstellen der ersten Ableitung berechnen

3. Intervalle benennen

4. Monotonietabelle aufstellen

5. Vorzeichen der Intervalle berechnen

6. Ergebnis interpretieren


Beispiel: Monotonieverhalten für bestimmen

Zuerst berechnen wir die Ableitung . Anschließend berechnen wir die Nullstellen der Ableitung () und erhalten durch Umformungen als Nullstelle .

Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten und . Darauffolgend stellen wir eine Monotonietabelle auf und berechnen die Vorzeichen für die Intervalle:
Graph von f Tiefpunkt

Aus dem Ergebnis können wir schließen, dass die Funktion für streng monoton fallend und für streng monoton steigend ist.


Aufgabe 2

a) Auf dem Bild siehst du den Graphen einer Ableitungsfunktion . Welche Aussagen kannst du über das Monotonieverhalten von machen?

















Erinnere dich daran, wie du bei der Berechnung des Monotonieverhaltens vorgehst. Welche Aussagen zum Monotonieverhalten liefert dir ?
Die Nullstellen von definieren die verschiedenen Intervalle, in denen das Monotonieverhalten von verschieden ist. Nun kannst du betrachten, auf welchen Intervallen bzw. ist. Welche Aussagen kannst du damit über das Monotonieverhalten von machen?

Die Nullstellen von sind und .

Damit sind die zu betrachtenden Intervalle , , und . Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob an diesen oder ist.

Für ist , somit ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} auf diesem Intervall streng monoton fallend.

Für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (-3, -2)} ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x)>0} , somit ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} auf diesem Intervall streng monoton steigend.

Für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (-2, -1)} ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x)<0} , somit ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} auf diesem Intervall streng monoton fallend.

Für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (-1, +\infty)} ist , somit ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} auf diesem Intervall streng monoton steigend.


b) Zeichne nun mithilfe deiner Ergebnisse aus a) den Funktionsgraphen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} mithilfe deiner Kenntnisse über sein Monotonieverhalten in dein Heft.

Dein Graph könnte in etwa so aussehen:

Graph f(x).jpg












Möglich, weitere Lösungen für die Zeichnung des Graphen sind unter anderem Verschiebungen in Richtung der Ordinate, also nach unten und oben oder auch Streckungen bzw. Stauchungen.


Aufgabe 3


a) Nach einem starken Regenschauer in Münster steigt der Wasserspiegel im Aasee an. Die Funktion beschreibt die Zuflussgeschwindkeit in den ersten 72 Stunden. Wann fließt innerhalb dieser Zeit Wasser zu und wann Wasser ab?

b)




Für Aufgabe 2a) Monotonietabelle

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle -\infty < x < 7,4 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x = 7,4 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 7,4 < x < 25,92 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x = 25,92 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 25,92 < x < \infty }
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g'(x) } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle > 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle < 0} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 0} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle > 0}
Graph von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \nearrow } Hochpunkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \searrow } Tiefpunkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \nearrow }


Für 2b)

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle -\infty < x < -\frac{\sqrt{15}}{5}a } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'\Big(-\frac{\sqrt{15}}{5}a \Big) } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle -\frac{\sqrt{15}}{5}a < x < 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'\Big(0\Big) } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0 < x < \frac{\sqrt{15}}{5}a } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'\Big(\frac{\sqrt{15}}{5}a \Big) } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{\sqrt{15}}{5}a < x < \infty}
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x) } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle < 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle > 0} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 0} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle < 0} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle > 0}
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle Graph von f } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \searrow } TP Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \nearrow } HP Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \searrow } TP Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \nearrow }


Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x=0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0 < x < \frac{\sqrt{15}}{5}a } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x=\frac{\sqrt{15}}{5}a } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{\sqrt{15}}{5}a < x \leq \ 4}
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f_a'(x) } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 0} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle < 0} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle > 0}
Graph von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f_a} HP Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \searrow } TP Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \nearrow }







Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle -\infty < x < -\frac{1}{3} } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'\Big(-\frac{1}{3}\Big) } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle -\frac{1}{3} < x < 1 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(1) } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1 < x < \infty }
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x) } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle > 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle < 0} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 0} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle > 0}
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle G_{f} } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \nearrow } Hochpunkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \searrow } Tiefpunkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \nearrow }
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle -\infty < x < 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x=0 }
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x) } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle < 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 0 } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle > 0}
Graph von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f } Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \searrow } Tiefpunkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \nearrow }
Abgerufen von „https://projektwiki.idea-sketch.com/index.php?title=Benutzer:Vivien_WWU-6/TestseiteAufgaben&oldid=21901“