Benutzer:Buss-Haskert/Gleichungen/Gleichungen mit Klammern

SEITE IM AUFBAU!!

zurück zur Seite der Herta-Lebenstein-Realschule

Gleichungen - Halte die Waage im Gleichgewicht

1.1) Was ist eine Gleichung
1.2) Gleichungen lösen durch Probieren
2) Gleichungen lösen durch Umformen
3) Gleichungen mit Klammern

4) Anwendungsaufgaben

Gleichungen mit Klammern lösen

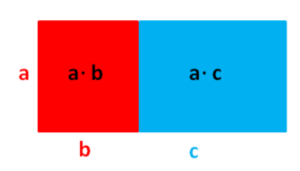
Vor der Klammer kann ein + Zeichen, ein - Zeichen oder ein Malzeichen stehen. Wiederhole, wie du jeweils die Klammer auflösen kannst.

Pluszeichen vor der Klammer

Steht in einer Summe oder Differenz ein Pluszeichen vor der Klammer, kannst du die Klammer einfach weglassen. Die Rechenzeichen im Term ändern sich nicht.

Merke dir als Bild den lachenden Smiley 🌝, denn diese Klammer aufzulösen ist sehr leicht!

Beispiele:

   2a + (3b + 4a)   |🌝 Klammer auflösen (weglassen)
= 2a + 3b + 4a   |gleichartige Terme zusammenfassen
= 6a + 3b

   -4x + (2y - 6x)   |🌝 Klammer auflösen (weglassen)
= -4x + 2y - 6x   |gleichartige Terme zusammenfassen
= -10x + 2y

Minuszeichen vor der Klammer

Steht in einer Summe oder Differenz ein Minuszeichen vor der Klammer, kannst du die Klammer auflösen, indem du die Rechenzeichen umdrehst:
aus + wird -
aus - wird +

Merke dir als Bild den Blitz , denn wenn du diese Klammer auflöst, musst du aufpassen!

Beispiele:

   5a - (6b + 7a)   |Klammer auflösen (Zeichen umkehren)
= 5a - 6b - 7a   |gleichartige Terme zusammenfassen
= -2a - 6b

   8x - (-9y - 4x)   |Klammer auflösen (Zeichen umkehren)
= 8x + 9y + 4x   |gleichartige Terme zusammenfassen
= 12x + 9y

Malzeichen vor der Klammer - Verteilungsgesetz (Distributivgesetz)

Steht in einer Summe oder Differenz ein Malzeichen vor der Klammer, löst du die Klammer auf, indem du jeden Summanden in der Klammer mit dem Faktor multiplizierst.
Merke dir als Bild die Hände , denn wenn du diese Klammer auflöst, musst der Faktor jedem Summanden "die Hand geben".

a ∙ (b + c) = a ∙ b + a ∙ c

Beispiele:

   2a ∙ (6b + 7a)   |Klammer auflösen ("Jedem die Hand geben")
= 2a ∙ 6b + 2a ∙ 7a   |Terme multiplizieren
= 12ab + 14a²

   5x ∙ (7y - 8x)   |Klammer auflösen ("Jedem die Hand geben")
= 5x ∙ 7y - 5x ∙ 8x   |Terme multiplizieren
= 35xy - 40x²

Übe das Auflösen von Klammern mithilfe der nachfolgenden LearningApp.

Gleichungen mit Klammern lösen

Gleichungen mit Klammern werden auch schrittweise gelöst.
Führe dazu zunächst Termumformungen auf beiden Seiten der Gleichung durch:
1. Löse die Klammern auf. (Denke an die entsprechenden Symbole: Smiley, Blitz, Hände)
2. Fasse die Terme auf beiden Seiten der Gleichung so weit wie möglich zusammen.

Löse anschließend die Gleichung schrittweise, wie geübt.

Gleichungen mit Klammern lösen

Bearbeite auf der Seite realmath die nachfolgenden Übungen

• Übung1
• Übung 2 (Löse nur die ersten 5 Aufgaben)
• Übung 3 (Löse nur die ersten 5 Aufgaben)

Übung 2

Löse die Aufgaben aus dem Buch. Schreibe hinter den Kommandostrich das Symbol zum Auflösen der Klammer. Löse anschließend die Klammer auf, fasse zusammen und löse die Gleichung. Vergleiche deine Lösungen und hake ab.

• S. 120 Nr. 1
• S. 120 Nr. 2
• S. 121 Nr. 3
• S. 121 Nr. 4

Lösungen (unsortiert):

-12; -6; -6; -3; 1; 2; 3; 3; 6; 6

Beispiel:
(4-5x)+(10+6x) = 8   |🌝 Klammer auflösen (weglassen)
4-5x+10+6x = 8   | sortieren
-5x+6x+4+10 = 8   | zusammenfassen
x+14 = 8   | -14
x = -6
Probe:
(4-5·(-6))+(10+6·(-6)) = 8
(4 + 30) + (10 - 36) = 8
34 - 26 = 8

8 = 8 (w)

Beispiel:
(x+6)·8 = 32x   |Klammer auflösen ("Jedem die Hand geben")
8·x + 8·6 = 32x
8x + 48 = 32x   |-8x
48 = 24x   | :24
2 = x
Probe:
(2+6)·8 = 32·2
8·8 = 64

64 = 64 (w)

Lösungen (unsortiert):

-2; -2; ${\tfrac {1}{2}}$; 1; 1,5; 3; 6; 6; 9

Übung 3

Löse auf der Seite Aufgabenfuchs mindestens 5 Aufgaben. Wähle aus.

• Nr. 31 - 38

Übung 4

Finde den Fehler! Schreibe die Aufgabe korrigiert in dein Heft.

• S. 121 Nr. 9

4) Anwendungsaufgaben