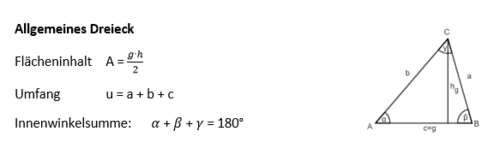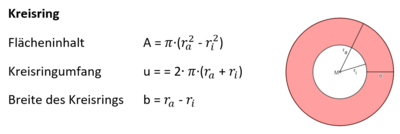Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Geometrie: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 175: | Zeile 175: | ||
</div> | </div> | ||
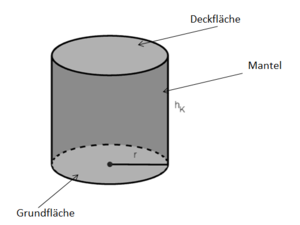
{{Box|Zylinder|[[Datei:Bezeichnungen am Zylinder .png|rechts|rahmenlos]]<br> | {{Box|1=Zylinder|2=[[Datei:Bezeichnungen am Zylinder .png|rechts|rahmenlos]]<br> | ||
Oberfläche: O = 2·G + M<br> | Oberfläche: O = 2·G + M<br> | ||
Volumen: V = G·h<sub>K</sub><br> | Volumen: V = G·h<sub>K</sub><br> | ||
Um die Grundfläche G eines Zyinders zu berechnen, nutze die Flächeninhaltsformel des Kreises.|Merksatz}} | Um die Grundfläche G eines Zyinders zu berechnen, nutze die Flächeninhaltsformel des Kreises.|3=Merksatz}} | ||
<ggb_applet id="y3gcvcfu" width="1139" height="702" border="888888" /> | <ggb_applet id="y3gcvcfu" width="1139" height="702" border="888888" /> | ||
<small>Applet von Jakob Pechmann</small>Originallink: https://www.geogebra.org/m/y3gcvcfu | <small>Applet von Jakob Pechmann</small>Originallink: https://www.geogebra.org/m/y3gcvcfu | ||
Version vom 11. Februar 2023, 14:01 Uhr
Geometrie
Winkel
1. Winkel zeichnen und messen
2. Winkel im Schnittpunkt von Geraden:
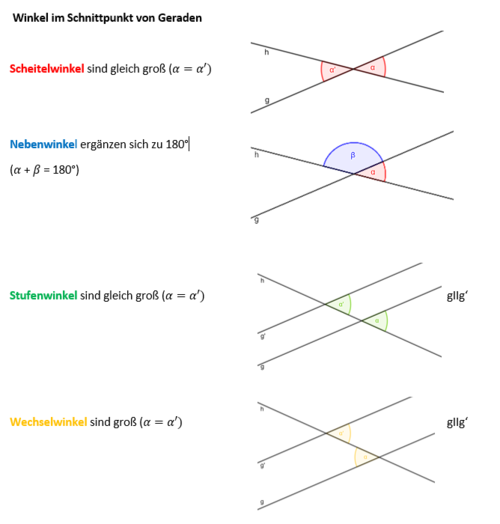
Dreiecke
Ist das Dreieck rechtwinklig, gilt der Satz des Pythagoras und die Trigonometrie!
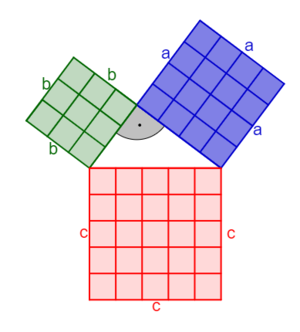
Satz den Pythagoras (in rechtwinkligen Dreiecken)
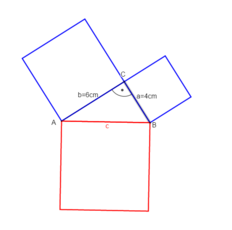
Beispiel 1: Die Katheten sind gegeben und die Hypotenuse ist gesucht.
geg: rechtwinkliges Dreieck mit γ=90°; Katheten: a = 4cm; b = 6cm
ges: Hypotenuse c
c² = a² + b² |
c = |Werte einsetzen
c = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sqrt{\text{4² + 6²}}}
|berechnen
(c = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sqrt{52}}
diesen Schritt musst du nicht notieren)
c Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \approx}
7,2 [cm]
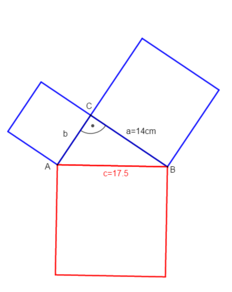
Beispiel 2: Die Hypotenuse und eine Kathete sind gegeben und die andere Kathete ist gesucht.
ges: Kathete b
a² + b² = c² |-a²
b² = c² - a² |Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \surd}
b = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sqrt{\text{c² - a²}}}
|Werte einsetzen
b = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sqrt{\text{17,5² - 14²}}}
|berechnen
(b = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sqrt{110,25}}
diesen Schritt musst du nicht notieren)
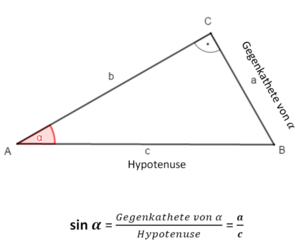
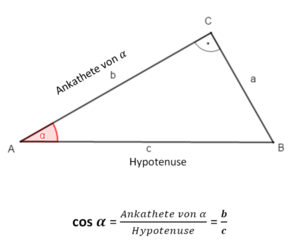
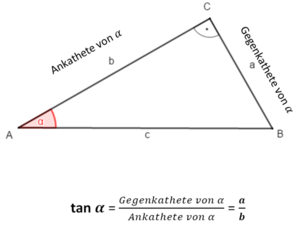
Trigonometrie (in rechtwinkligen Dreiecken)
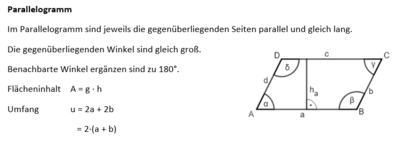
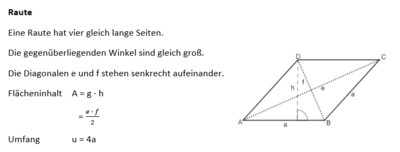
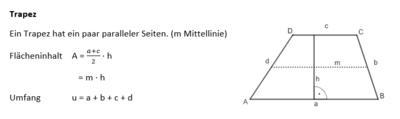
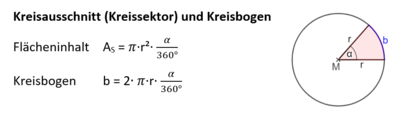
Ebene Figuren
Ist das Dreieck rechtwinklig, gilt der Satz des Pythagoras und die Trigonometrie!
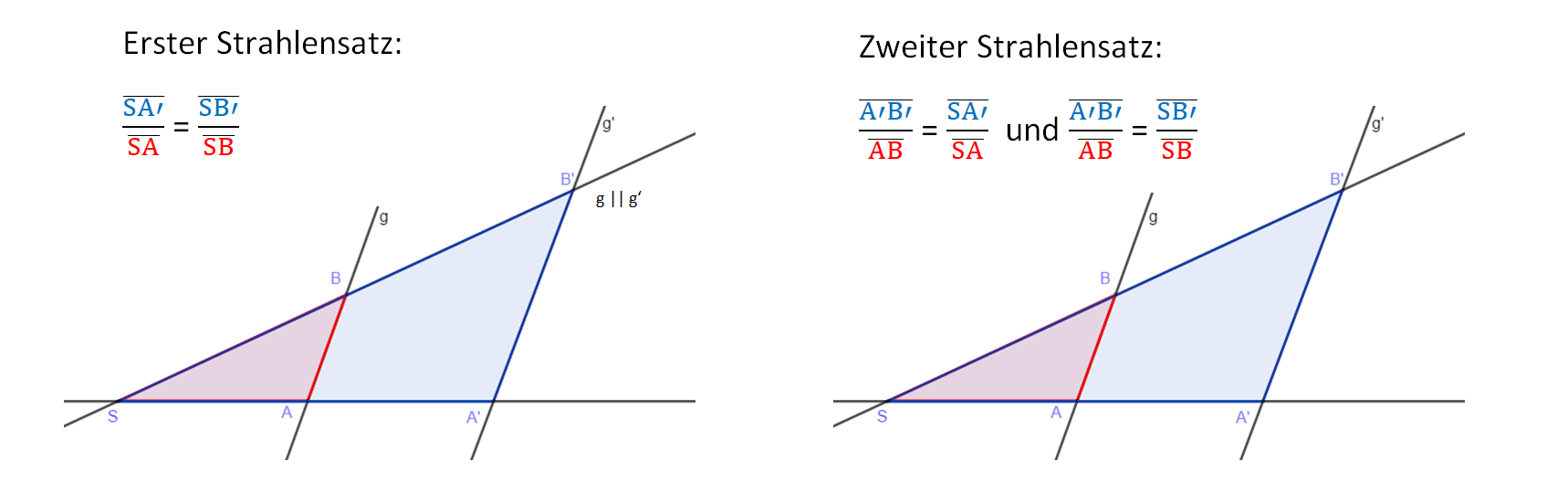
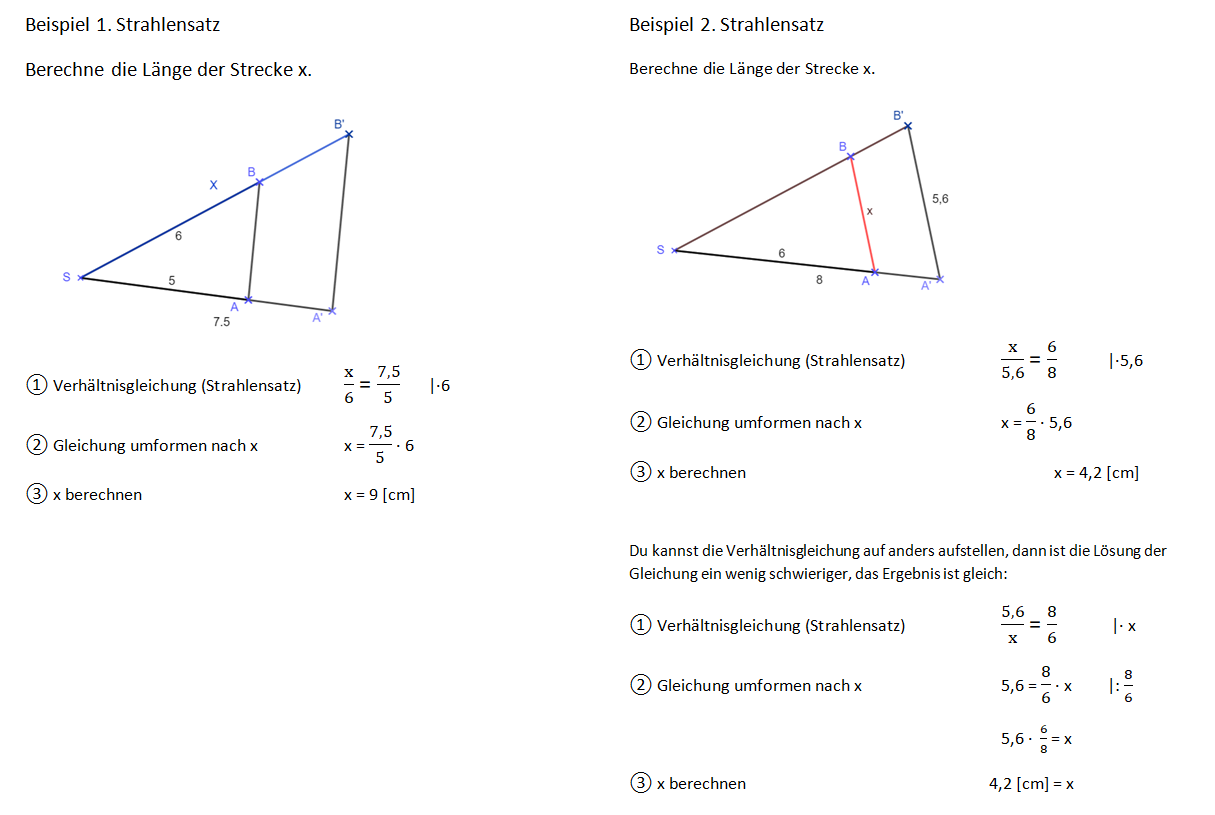
Strahlensätze
Längen mit den Strahlensätzen zu berechnen, gehen wir schrittweise vor.
Körperberechnungen
Applet von Hegius
Applet von Jakob PechmannOriginallink: https://www.geogebra.org/m/y3gcvcfu
