Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren/Quadratische Funktionen

Info

In diesem Lernpfad geht es darum, dein Wissen im Bereich quadratischer Funktionen zu vertiefen.

Dazu werden dir Informationen und Aufgaben zur Scheitelpunktform, der Umwandlung zwischen Scheitelpunktform und Normalform sowie zur Berechnung von Nullstellen bereitgestellt. Zusätzlich erwarten dich zwei Anwendungsaufgaben, in welchen du die zuvor gelernten Inhalte testen kannst.

In diesem Lernpfad findest du Aufgaben mit einem *. Bei diesen handelt es sich um Forderaufgaben. Aufgaben mit ** sind anspruchsvolle Knobelaufgaben. Hat eine Aufgabe kein *, dann ist die Aufgabe zur Wiederholung und Vertiefung der Inhalte geeignet.

Scheitelpunktform

1. Parameter der Scheitelpunktform

Fülle den folgenden Lückentext aus, indem du die passenden Silben einfügst.

Wir schauen uns die Funktion $g(x)=a*(x-d)^{2}+e$ an. Funktionen dieser Art heißen qua dra tisch e Funktionen. Der Graph einer solchen Funktion ist eine Pa ra bel. Der höchste bzw. der tiefste Punkt eines solchen Funktionsgraphen heißt Schei tel punkt. Liegt die Funktionsgleichung in der Scheitelpunktform vor, wie es hier der Fall ist, dann kann der Scheitelpunkt S direkt aus der Funktionsgleichung abgelesen werden. Der Parameter d ist die x-Koordinate und der Parameter e ist die y-Koordinate des Scheitelpunkts. $\Rightarrow$ S(d,e).
Ist der Parameter a kleiner als Null (a<0), dann ist der Graph der Funktion g nach un ten geöffnet.
Ist a größer als Null (a>0), dann ist der Graph von g nach o ben geöffnet.
Ist a größer als Eins (a>1) oder kleiner als minus Eins (a<-1), dann sieht der Graph von g schma ler aus. Man sagt, dass in diesem Fall der Graph ge streckt wird.
Liegt a zwischen minus Eins und Eins (-1<a<1), dann sieht der Graph von g brei ter aus. Man sagt, dass in diesem Fall der Graph ge staucht wird.

Ist d größer als Null (d>0), dann wird der Graph von g nach rechts verschoben.
Ist d kleiner als Null (d<0), dann wird der Graph von g nach links verschoben.

Ist e kleiner als Null (e<0), dann wird der Graph von g nach un ten verschoben.
Ist e größer als Null (e>0), dann wird der Graph von g nach o ben verschoben.

2.WANTED! Welche Punkte gehören nicht zu der Funktion f?

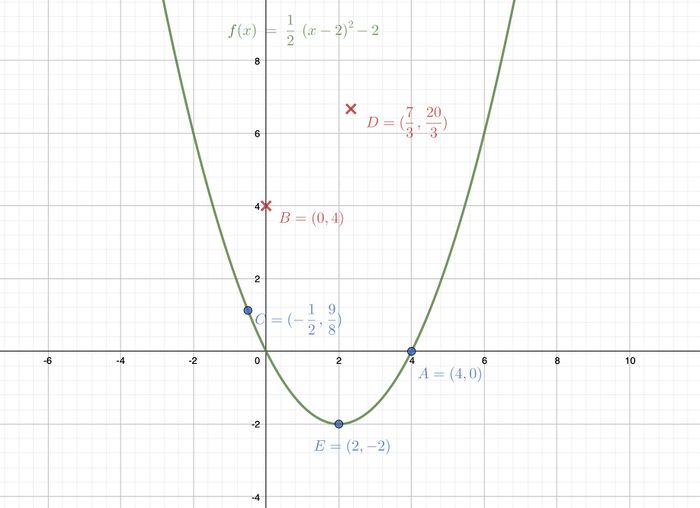
Gegeben seien die Funktion $f(x)=-{\frac {1}{2}}\cdot (x-2)^{2}-2$ und die Punkte $A=(4,0),$ $B=(0,2),$ $C=(-{\frac {1}{2}},{\frac {9}{8}}),$ $D=({\frac {7}{3}},{\frac {20}{3}})$ und $E=(2,-2)$.

a) Überprüfe rechnerisch, ob die Punkte A, B, C, D und E auf dem Graphen von f liegen.

b) Zeichne den Graphen der Funktion f und die Punkte A-E in dein Heft. Vergleiche anschließend die Ergebnisse aus a) mit deiner Zeichnung

Du kannst einfach prüfen, ob ein Punkt auf dem Graphen liegt: Setze den x-Wert in die Funktionsgleichung ein und berechne den zugehörigen y-Wert

Du hast Probleme beim Zeichnen des Graphen? Der Lückentext in Aufgabe 1 hilft dir weiter.

Starte beim Zeichnen mit dem Scheitelpunkt, den du aus der Funktionsgleichung ablesen kannst. Auch hierbei kann dir Aufgabe 1 helfen.

Beim Zeichnen des Funktionsgraphen gibt dir der Parameter a an, wie viele Einheiten du nach oben oder unten "gehen" musst, wenn du eine Einheit nach rechts oder links "gehst".

Wenn deine Zeichnung so aussieht, hast du alles richtig gemacht:

3. Welcher Graph hat mit welcher Funktionsgleichung ein Match?

Ordne die folgenden Funktionsgleichungen den zugehörigen Graphen zu. Hinweis: Du kannst das Bild der Funktionsgraphen vergrößern, indem du mit der Maus auf diese klickst.

a steht für die Verschiebung in X-Richtung.

b für die Verschiebung in Y-Richtung.

Beispiele sind:

$f(x)=(x-3)^{2}+2$ hat ihren Scheitelpunkt bei (3, 2)

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)=(x+0)^2-4} hat ihren Scheitelpunkt bei (0, -4)

4. Aus dem Graphen eine quadratische Funktion in Scheitelpunktform aufstellen

Stell die zugehörigen Funktionsgleichungen in Scheitelpunktsform auf. Wähle im Anschluss die richtige Lösung aus.

Überlege dir zunächst, welche Parameter du brauchst um eine Funktionsgleichung in Scheitelpunktform aufzustellen. (Falls du Aufgabe 1 schon bearbeitet hast, findest du dort nützliche Hinweise.)

Die Scheitelpunktform hat die Funktionsgleichung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot(x-d)^2+e} . Probiere aus was passiert, wenn du die Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a, d} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle e} veränderst. Beobachte die Funktionsgleichung und den zugehörigen Graphen.

Für den Scheitelpunkt gilt: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle S=(d,e)} . Wenn du also den Scheitelpunkt aus der Darstellung des Funktionsgraphen abliest und seine Koordinaten in die Funktionsgleichung einsetzt, musst du nur noch den Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a} bestimmen.

Um den Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a} zu bestimmen gibt es verschiedene Möglichkeiten.

Möglichkeit 1: Du kannst einen beliebigen weiteren Punkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (x,y} ) aus dem Graphen ablesen und in die Funktionsgleichung einsetzen. Im Anschluss musst du nur noch die Gleichung nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a} auflösen. Bei Bedarf kannst Du gerne dein Heft benutzen, um dir Rechenschritte zu notieren.

Möglichkeit 2: Alternativ kannst du den Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a} auch direkt aus dem Graphen ablesen: Gehst du vom Scheitelpunkt aus um eine Einheit nach rechts, so entspricht Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a} der Anzahl an Einheiten, die du nach oben (positives Vorzeichen) oder nach unten (negatives Vorzeichen) gehen musst, bis du wieder auf dem Graphen bist.

5. Anwendungsaufgabe für Zwischendurch: Flugbahn eines Steins

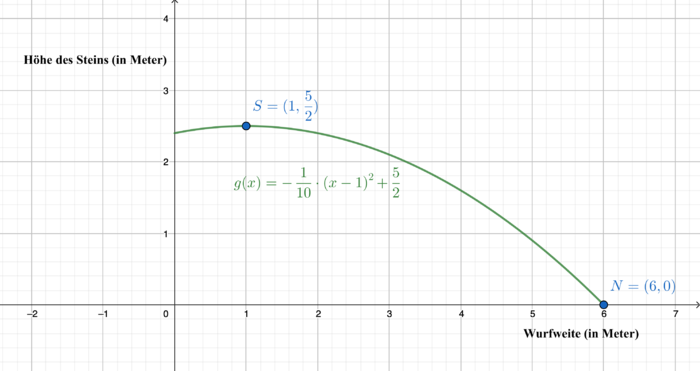
Jonas wirft einen Stein vom Ufer in einen See. Die Flugbahn des Steins lässt sich mit der quadratischen Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)=-\frac{1}{10}\cdot(x-1)^2+\frac{5}{2}} beschreiben, wobei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} die Entfernung des Steins vom Ufer und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)} die Höhe des Steins (jeweils in Meter) beschreibt.

a) An welcher Stelle erreicht der Stein seinen höchsten Punkt?

b) Zeichne die Flugbahn des Steins in dein Heft.

c)* Wie weit fliegt der Stein?

Der Stein erreicht seinen höchsten Punkt am Scheitelpunkt der Funktion. Da die Funktion in Scheitelpunktform angegeben ist, kannst du diesen direkt aus der Funktionsgleichung ablesen.

Zu Erinnerung: Eine quadratische Funktion in Scheitelpunktform hat die Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)=a\cdot(x-d)^2+e} . Um die Flugbahn zeichnen zu können, musst du die Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a,d} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle e} der gegebenen Funktionsgleichung identifizieren.

Zeichne zunächst den Scheitelpunkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle S=(d,e)} ein. Beim weiteren Zeichnen des Funktionsgraphen gibt dir der Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a} an, wie viele Einheiten (Meter) du nach oben oder unten "gehen" musst, wenn du eine Einheit (Meter) nach rechts oder links "gehst".

Um diesen Aufgabenteil zu lösen, musst du die Nullstellen der Funktion bestimmen (an einer dieser Nullstellen trifft der Stein auf das Wasser). Falls du dich dabei noch unsicher fühlst, bearbeite zuerst Aufgabe 9. Dort findest Du alle notwendigen Hilfestellungen. In jedem Fall solltest du für die Rechenschritte dein Heft benutzen.

Der Scheitelpunkt der Funktion ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle S=(1,\frac{5}{2})} . Der Stein erreicht seinen höchsten Punkt also bereits nach einem Meter.

Beachte, dass die Flugbahn erst mit dem Abwurf des Steins beginnt und mit dem Auftreffen des Steins auf dem See endet. Auf der X-Achse trägst du die Wurfweite in Meter ab, auf der Y-Achse die Höhe des Steins in Meter.

Du musst zunächst die Nullstellen der Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)} bestimmen. An einer dieser Nullstellen trifft der Stein auf die Wasseroberfläche.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} && g(x) &&=&& 0 \\ &\Leftrightarrow& 0 &&=&& -\frac{1}{10}\cdot(x-1)^2+\frac{5}{2} &\mid \cdot(-10)\\ &\Leftrightarrow& 0 &&=&& (x-1)^2-25 &\mid +25 \\ &\Leftrightarrow& 25 &&=&& (x-1)^2 &\mid \sqrt{} \\ \end{array} }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &\Rightarrow&(x_1-1) = -5& \textrm{sowie}& (x_2-1)=5\\ \end{array} }

Also folgt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_1=-4} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_2=6} . Damit haben wir zwei Nullstellen.

Da wir jedoch davon ausgehen, dass Jonas den Stein nach vorne in den See wirft, beträgt die Wurfweite 6 m.

Umwandlung Scheitelpunktform und Normalform

Bisher hast du dich intensiv mit der Scheitelpunktform beschäftigt. In diesem Abschnitt wirst du auch mit der Normalform einer quadratischen Funktion arbeiten. Dafür benötigst du die ersten beiden Binomischen Formeln. In dem folgenden Merksatz sind diese dargestellt. Falls du bei den nachfolgenden Aufgaben Schwierigkeiten bei der Umwandlung der Binomischen Formeln hast, dann scroll bis zu diesem Merksatz hoch und schau ihn dir nochmal an.

Die ersten beiden Binomischen Formeln

1. Binomische Formel: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (a+b)^2=a^2+2ab+b^2 }

2. Binomische Formel: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (a-b)^2=a^2-2ab+b^2 }

6. Die Umwandlungen zwischen Scheitelpunktform und Normalenform

Fülle den Lückentext aus, indem du auf eine Lücke klickst und die richtige Antwort auswählst.

7. Wie ging noch einmal quadratische Ergänzung?

Fülle den Lückentext aus, indem du auf eine Lücke klickst und die richtige Antwort auswählst.

8. Finde die Paare*

Wandle in deinem Heft die Funktionen f und g in die Normalform um und die Funktionen i und j in die Scheitelpunktform. Ordne anschließend die gleichen Funktionen einander zu.
Hinweis: Es bleiben am Ende drei Funktionsgleichungen übrig.

Wenn du dir nicht mehr genau weißt, wie du von der Scheitelpunktform in die Normalform kommst oder umgekehrt, dann schau dir nochmal die Aufgaben 6 und 7 an.

[Lösung anzeigen][Lösung ausblenden]

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} f(x) &=& (x+3)^2+4 &\mid \, 1. \, Binomische \, Formel \\ &=& (x^2+6x+9)+4 &\mid \, zusammenfassen \\ &=& x^2 +6x +13 \end{array} }

[Lösung anzeigen][Lösung ausblenden]

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} g(x) &=& 2 \cdot (x-3)^2+9 &\mid \, 2. \, Binomische \, Formel \\ &=& 2 \cdot (x^2 -6x +9)+9 &\mid \, ausmultiplizieren \\ &=& 2x^2-12x+18+9 &\mid zusammenfassen \\ &=& 2x^2-12x+27 \end{array} }

[Lösung anzeigen][Lösung ausblenden]

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} h(x) &=& x^2-14x-4 &\mid \, quadratische \, Erg\ddot{a}nzung \\ &=& x^2-14x +7^2-7^2-4 &\mid \, 2. \, Binomische \, Formel \, r\ddot{u}ckw\ddot{a}rts \, anwenden \\ &=& (x-7)^2-7^2-4 &\mid \, zusammenfassen \\ &=& (x-7)^2 -53 \end{array} }

[Lösung anzeigen][Lösung ausblenden]

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} i(x) &=& -2 \cdot x^2 -12x -11 &\mid \, (-2) \, ausklammern \\ &=& -2 \cdot [x^2+6x+\frac{11}{2}] &\mid \, quadratische\, Erg\ddot{a}nzung \\ &=& -2 \cdot [x^2+6x+3^2-3^2+\frac{11}{2}] &\mid \, 1. \, Binomische \, Formel \, r\ddot{u}ckw\ddot{a}rts \, anwenden \\ &=& -2 \cdot [(x+3)^2-9+\frac{11}{2}] &\mid \, zusammenfassen \\ &=& -2 \cdot [(x+3)^2-\frac{7}{2}] &\mid \, ausmultiplizieren \\ &=& -2 \cdot (x+3)^2 +7 \end{array} }

9. Würdest du bei der Umwandlung zwischen der Scheitelpunktform und der Normalform auch Millionär werden?**

Wähle die Antwortmöglichkeit A,B,C oder D, welche die angefangene Gleichung zu einer korrekten quadratischen Gleichung ergänzt.

Die zum lösen benötigten Formeln sind die binomischen Formeln.

Die binomischen Formeln lauten:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (a+b)^2=a^2+2*ab+b^2}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (a-b)^2=a^2-2*ab+b^2}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (a+b)*(a-b)=a^2-b^2}

Nullstellen

10. Nullstellen berechnen

Bestimme jeweils die Nullstellen:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)=-3(x-1)^2+3 }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)=2x^2-8x+6 }

Da einige Rechenschritte notwendig sind, solltest du dein Heft benutzen.

Überlege dir zunächst, wie Nullstellen definiert sind. Aus der Definition kannst Du direkt den ersten Schritt zur Nullstellenbestimmung ableiten.

Zur Erinnerung: Nullstellen sind diejenigen x-Werte, die eingesetzt in die Funktion 0 ergeben. Setze also zunächst Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)=0} bzw. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)=0}

Es gibt unterschiedliche Möglichkeiten, diese Gleichung aufzulösen: Bei einer Funktion in Scheitelpunktform hilft es in der Regel, den Term Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (x-d)^2} auf einer Seite zu isolieren und dann auf beiden Seiten die Wurzel zu ziehen.

Weitere nützliche Hilfsmittel sind pq-Formel, quadratische Ergänzung und Mitternachtsformel.

Überlege dir jeweils, welcher Weg für die konkrete Aufgabenstellung am sinnvollsten ist.

Im Unterricht habt ihr sicherlich die pq-Formel kennengelernt. Diese besagt:

Eine Gleichung der Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x^2+px+q=0} hat die Lösungen

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_{1} = -\frac{p}{2}-\sqrt{\left( \frac{p}{2}\right)^2-q}} sowie Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_{2} = -\frac{p}{2}+\sqrt{\left( \frac{p}{2}\right)^2-q}}

Die pq-Formel ist z.B. für die Bestimmung der Nullstellen von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} sehr nützlich.

Eine Möglichkeit die Nullstellen von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)} zu bestimmen lautet wie folgt:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} && g(x) &&=&& 0 \\ &\Leftrightarrow& 0 &&=&& -3(x-1)^2+3 &\mid :(-3) \\ &\Leftrightarrow& 0 &&=&& (x-1)^2-1 &\mid +1 \\ &\Leftrightarrow& 1 &&=&& (x-1)^2 &\mid \sqrt{} \\ \end{array} }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} &\Rightarrow&(x_1-1) = -1& \textrm{sowie}& (x_2-1)=1\\ \end{array} }

Also folgt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_1=2} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_2=0} . Das sind die Nullstellen.

Diese Funktion ist in Normalform angegeben. Du kannst also nach wenigen Rechenschritten auf die pq-Formel zurückgreifen, um die Nullstellen zu bestimmen:

Betrachte Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)=0 } , d.h. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0 = 2x^2-8x+6} und teile dann beide Seiten durch Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 2} .

Du erhälst die Gleichung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0 = x^2-4x+3}

Durch Anwenden der pq-Formel folgt


⇔ Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_{1} = -\frac{-4}{2}-\sqrt{\left( \frac{-4}{2}\right)^2-3}} sowie Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_{2} = -\frac{-4}{2}+\sqrt{\left( \frac{-4}{2}\right)^2-3}}

⇔ Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_1 = 2-1} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_2 = 2+1}

Somit sind Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_1=1} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_2=3} die Nullstellen.

Anwendungsaufgabe

11. Baseball

Baseball ist eine der beliebtesten Sportarten der Welt. Beim Wurf erreicht der Ball Geschwindigkeiten bis zu 160km/h. Wenn der Schlagmann den Ball richtig trifft, kann dieser über die Tribüne hinweg aus dem Stadion fliegen. Ein bestimmter Schlag kann durch die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle j(x)=-0,0075x^2+1,2x+1} beschrieben werden, wobei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} die horizontale Entfernung zum Schlagmann und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle j(x)} die Höhe des Balls, jeweils in Meter angibt.

a) Berechne j(0) und beschreibe, was dieser Wert im Anwendungskontext bedeutet.

Lies in der Aufgabenstellung noch einmal nach, wofür Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle j(x)} stehen.

Was bedeutet es, wenn x=0 ist?

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rll} j(0) &=& -0.0075 \cdot 0^2 + 1.2 \cdot + 1 \\ &=& 1 \end{array} }

Der Schlagmann trifft den Baseball einen Meter über dem Boden.

b) Ein Spieler des gegnerischen Teams befindet sich 158 Meter vom Schlagmann entfernt in der Flugbahn des Balls. Wenn er hochspringt, erreichen seine Händen eine Höhe von 3,20 Metern. Berechne, ob der Spieler es schafft, den Ball aus der Luft zu fangen.

Berechne die Höhe des Balls nach 158 Metern und vergleiche diese Höhe mit der maximalen Sprunghöhe des Gegenspielers.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rll} j(158) &=& -0.0075 \cdot 158^2+ 1.2 \cdot 158 + 1 \\ &=& 3.37 \end{array} }

Auf Höhe des gegnerischen Spielers hat der Baseball noch eine Höhe von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 3.37m.} Da der Spieler nur Bälle bis zu einer Höhe von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 3.20m} erreichen kann, fängt er diesen Ball nicht.

c) Berechne, wie weit der Baseball fliegt, wenn er von keinem gegnerischen Spieler aus der Luft gefangen wird.

Überlege dir, welchen Wert Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle j(x)} annehmen muss, wenn der Baseball auf dem Boden aufkommt.

Setze Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle j(x)=0} und berechne die Nullstellen.

Falls du nicht mehr genau weißt, wie du die pq-Formel aufstellen und berechnen kannst, dann schau nochmal in Tipp 3 von Aufgabe 10 nach. Achte darauf, dass vor dem Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x^2} kein Vorfaktor stehen darf.

Nullstellenberechnung:
Im ersten Schritt wird der Vorfaktor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x^2} eliminiert.
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 0 &=& -0.0075 \cdot x^2 + 1.2 \cdot x + 1 & \mid :(-0.0075) \\ &=& x^2 - 160x - \frac{400}{3} \end{array} }

Im zweiten Schritt wird die pq-Formel angewendet, um die Nullstellen zu berechnen.
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow p=-160, q= -\frac{400}{3} }
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} x_{1/2} &=& -\frac{-160}{2} \pm \sqrt{{\left( \frac{-160}{2} \right)}^2 -(-\frac{400}{3}} \\ &=& 80 \pm \sqrt{\frac{19600}{3}} \\ &=& 80 \pm 80.83 \\ \end{array} }
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow x_1 = 80+80.83 = 160.83 } und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_2 = 80-80.83 = -0.83 } Der Zeitpunkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_2} liegt zeitlich vor dem Schlag. Aus diesem Grund müssen wir nur Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_1} betrachten. Somit fliegt der Baseball Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 160.83} Meter weit, bevor er auf dem Boden fällt.

d) Nach wieviel Metern erreicht der Baseball seine maximale Höhe? Welche Höhe erreicht er?

Überlege dir, an welchem Punkt der Flugkurve der Baseball am höchsten ist.

Gesucht ist der Scheitelpunkt von der Funktion.

Überlege, wo du den Scheitelpunkt ablesen kannst.

Wenn du gerade nicht mehr darauf kommst, wie du aus der Normalform einer quadratischen Funktion in die Scheitelpunktform kommst, dann guck dir nochmal die Aufgabe 7 an.

Umwandlung der Normalform in die Scheitelpunktform:
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} j(x) &=& -0.0075 \cdot x^2 + 1.2 \cdot x +1 &\mid -0.0075 \, ausklammern \\ &=& -0.0075 (x^2-160x-\frac{400}{3}) &\mid +80^2 -80^2 \, quadratische \, Erg\ddot{a}nzung\\ &=& -0.0075 (x^2-160x + 80^2-80^2-\frac{400}{3}) &\mid 2. \, binomische \, Formel\\ &=& -0.0075 [(x-80)^2 -\frac{19600}{3}] &\mid ausmultiplizieren \\ &=& -0.0075 (x-80)^2 +49 \end{array} }
Der Scheitelpunkt liegt bei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle S(80 \mid 49).} Somit erreicht der Baseball nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 80} Metern die maximale Höhe von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 49} Metern.

e)** Berechne die horizontale Entfernung zum Schlagmann, in welcher der Baseball eine Höhe von 0,5 Metern hat.

Gesucht werden die x-Werte, sodass Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle j(x)=0.5} ist.

Setze anstelle von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle j(x)} den Wert 30 in die Funktion ein und löse die Gleichung nach x auf.

Bringe alles auf eine Seite und löse dann die Gleichung mit der p-q-Formel.

Wir müssen für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle j(x)=0.5} die zugehörigen x-Werte berechnen. Dafür setzen wir Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0.5} für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle j(x)} ein und bringen als erstes alle Summanden auf eine Seite.
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 0.5 &=& -0.0075 \cdot x^2 + 1.2 \cdot x + 1 \mid -0.5 \\ \Leftrightarrow 0&=&-0.0075 \cdot x^2 + 1.2 \cdot x +0.5 \end{array} }

Als nächstes eliminieren wir den Vorfaktor vor Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x^2.}
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rlll} 0 &=& -0.0075 \cdot x^2 + 1.2 \cdot x +0.5 &\mid :(-0.0075) \\ &=& x^2 -160 \cdot x - \frac{200}{3} \end{array} }

Nun lösen wir die Gleichung mithilfe der pq-Formel nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} auf.
Es gilt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle p=-160, q= -\frac{200}{3}.}
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rll} x_{1/2} &=& -\frac{-160}{2} \pm \sqrt{ \left( \frac{-160}{2} \right)^2 + \frac{200}{3}} \\ &=& 80 \pm \sqrt{\frac{19400}{3}}\\ &=& 80 \pm 80.42 \end{array} }
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow x_1 = 80+80.42 = 160.42 } und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_2 = 80-80.42 = -0.42 }

Der Baseball hat nach ungefähr Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 160.42} Metern eine Flughöhe von 0,5 Metern.