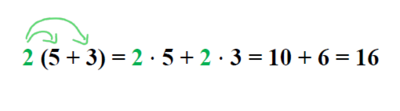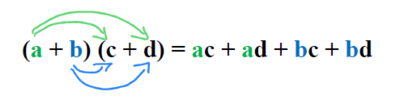Digitale Werkzeuge in der Schule/Fit für VERA-8/Terme

Info

In diesem Lernpfadkapitel lernst du Grundlagen über Terme und binomische Formeln kennen. Kurzbeschreibung des Aufbaus.Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.

Viel Erfolg!

1) Terme zusammenfassen

Einführung

Wie kann ich Terme zusammenfassen?

Rechenregeln

Terme erhalten unterschiedliche Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division. Manche Teile von Termen kann man zusammenfassen, um so den Term zu vereinfachen. Beachte dabei: 

Beim Zusammenfassen von Summen gilt:
Nur gleiche Variablen in der gleichen Potenz dürfen zusammengefasst werden.
Beispiele:
$2a^{2}+a+3a$
$=2a^{2}+4a$

$2x+xy-3y^{2}-2xy+2xy^{2}$
$=2x-3y^{2}+2xy^{2}+(xy-2xy)$
$=2x-3y^{2}+2xy^{2}-xy$
Hier konnten nur die beiden Teile mit xy zusammengefasst werden, da alle anderen Variablen unterschiedlich sind bzw. in einer anderen Potenz vorkommen.

$2x+4y-xy+2y-3x+5xy$
$=-x+6y+4xy$
Tipp: Es kann helfen die gleichen Potenzen und Variablen farblich zu markieren.

Beim Zusammenfassen von Produkten gilt:
Es können auch Teile mit unterschiedlichen Potenzen oder Variablen zusammengefasst werden.
Beispiel:
$2x\cdot 4xy$
$=2\cdot x\cdot 4\cdot x\cdot y$
$=2\cdot 4\cdot x\cdot x\cdot y$
$=8\cdot x^{2}\cdot y$
$=8x^{2}y$

Beachte die Vorzeichen der Faktoren.

$(-x)+(-x)=2x$
$(-x)\cdot (-y)=x\cdot y$

Beachte außerdem: Punkt- vor Strichrechnung, die Klammer geht immer vor.

Beispiel:
$2x\cdot (-7x^{2}y)\cdot (-3y^{3})$
$2\cdot (-7)\cdot (-3)\cdot x\cdot x^{2}\cdot y\cdot y^{3}$
$42x^{3}y^{4}$

Aufgabenteil

Aufgabe 1:

Aufgabe 2:

Fasse den folgenden Term zusammen: 

$4x-({1 \over 4}y-(5x+3z)-(x+{5 \over 8}y-2z))$

Zuerst musst du die Klammern auflösen, dann die Summanden nach ihren Variablen ordnen. Danach musst du noch die Brüche gleichnamig machen um danach alles zusammenfassen zu können.

$10x+{3 \over 8}y+z$

$4x-({1 \over 4}y-(5x+3z)-(x+{5 \over 8}y-2z))$
$=4x-({1 \over 4}y-5x-3z)-x-{5 \over 8}y+2z))$
$=4x-{1 \over 4}y+5x+3z+x+{5 \over 8}y-2z$
$=4x+5x+x-{1 \over 4}y+{5 \over 8}y+3z-2z$
$=4x+5x+x-{2 \over 8}y+{5 \over 8}y+3z-2z$

$=10x+{3 \over 8}y+z$

Aufgabe 3:

Das magische Quadrat: Die Summe jeder Zeile, Spalte und Diagonale des magischen Quadrats ergeben gleichwertige Terme. Ergänze die fehlenden Terme.

magisches Quadrat

5a+5
a+2	3a+1
3a-4

Berechne zuerst die Summe der ersten Spalte. Diese Summe muss auch die Summe aller weiteren Zeilen, Spalten und Diagonalen sein

Wenn du die Summe der ersten Spalte berechnet hast, kannst du als nächstes die Summe der zweiten Zeile berechnen und in das noch auszufüllende Kästchen der zweiten Zeile den Term eintragen, der in der Summe noch fehlt, damit die Summe der ersten Spalt gleich der Summe der zweiten Zeile ist.

{

}

2) Terme ausmultiplizieren und faktorisieren

Terme ausmultiplizieren

Titel

Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen. Um einen Faktor (im Bsp. 2) mit einer Klammer, in der eine Summe oder Differenz steht (im Bsp. 5 + 3), zu multiplizieren, muss der Faktor mit jedem Glied in der Klammer multipliziert werden:

Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht:

$(5+3){\color {green}2}=5\cdot {\color {green}2}+3\cdot {\color {green}2}=10+6=16$.

Achte darauf, ob in der Klammer eine Summe oder Differenz steht, denn:

$2(5{\color {red}-}3)=2\cdot 5{\color {red}-}2\cdot 3=10{\color {red}-}6=4$.

Die gleichen Rechenregeln gelten für Variablen:

${\color {green}a}(b+c)={\color {green}a}b+{\color {green}a}c$.

Das kann man sich auch anhand von Flächen mit den Seitenlängen a, b und c veranschaulichen:

Besonders aufpassen muss man bei Minusklammern, also wenn vor der Klammer ein negativer Faktor steht. Denn dann drehen sich die Vorzeichen von jedem Glied in der Klammer um:

${\color {red}-}a(b{\color {red}+}c)={\color {red}-}ab{\color {red}-}ac$.

${\color {red}-}a({\color {red}-}b{\color {red}+}c)=ab{\color {red}-}ac$.

Hierfür gilt:
$+\cdot +$ ergibt: $+$
$-\cdot -$ ergibt: $+$

$-\cdot +$ ergibt: $-$

Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:

${\color {green}x}(3+2)=3{\color {green}x}+2{\color {green}x}=5{\color {green}x}$.

${\color {green}2}(3x-1)={\color {green}2}\cdot 3x-{\color {green}2}\cdot 1=6x-2$.

${\color {red}-}(a{\color {red}+}b)={\color {red}-}a{\color {red}-}b$.

${\color {red}-}(a{\color {red}-}b)={\color {red}-}a{\color {red}+}b$.

Aufgabe

Aufgabe 1

In dieser Aufgabe kannst du nun das eben Gelernte üben. Dazu sollst du jedem Klammerterm, die korrekte ausmultiplizierte Lösung zuordnen. Nimm dir einen Zettel für Nebenrechnungen zur Hilfe.

a) $-a(b-c)=$ $-ab+ac$
b) $4(5a+4b)=$ $20a+16b$
c) $-8(a+2b)=$ $-8a-16b$
d) $10(5a+6b+3c)=$ $50a+60b+30c$
e) $(5a+10b)({\frac {1}{5}}c+2d)=$ $ac+10ad+2bc+20bd$
f) ${\frac {1}{2}}({\frac {1}{2}}a+{\frac {1}{3}}b)=$ ${\frac {1}{4}}a+{\frac {1}{6}}b$
g) $-{\frac {1}{4}}(a+b)$ = $-{\frac {1}{4}}a-{\frac {1}{4}}b$
h) $({\frac {1}{2}}a+{\frac {1}{2}}b)(2c+4d)$ = $ac+2ad+bc+2bd$

Terme faktorisieren

Titel

Beim Faktorisieren (auch genannt: Ausklammern) geht es genau umgekehrt wie beim Ausmultiplizieren darum, eine Klammer zu erstellen. Wie das funktioniert, erklärt dir Lehrer Schmidt in folgendem Video: [1]

${\color {green}2}a+{\color {green}2}b={\color {green}2}(a+b)$
${\color {green}4}x+{\color {green}4}y={\color {green}4}(x+y)$
$16x+4y={\color {green}4}\cdot 4x+{\color {green}4}y={\color {green}4}(4x+y)$

$6a+3b+12c={\color {green}3}\cdot 2a+{\color {green}3}b+{\color {green}3}\cdot 4c={\color {green}3}(2a+b+4c)$

Um zu überprüfen, ob du richtig faktorisiert hast, kannst du eine Probe durchführen, indem du deinen faktorisierten Term ausmultiplizierst und schaust, ob der Ursprungsterm herauskommt.

Aufgabe

a) $3\cdot x+12$

Weitere Aufgaben

Aufgabe 3

Welche Zahl muss man einsetzen, damit die Umformung stimmt?

a) 3() $\cdot (2\cdot x+7)=6\cdot x+21$
b) 15() $\cdot x+35=5\cdot (3\cdot x+7)$
c) $4\cdot (-3\cdot z+2)=$ -12() $\cdot z+8$
d) $9\cdot y-15=3\cdot (3\cdot y$ -5() $)$
e) $(-24\cdot a+42)\cdot {\frac {1}{6}}=$ -4() $a+$ 7()

Aufgabe 4

In dieser Aufgabe geht es darum, das Gelernte möglichst schnell anzuwenden, denn du trittst gegen den Computergegner an 😉 wer gewinnt das Rennen?

3) Binomische Formeln

Einführung

Was sind die binomischen Formeln?

Definition

Die folgenden drei Umformungen bilden die sogenannten binomischen Formeln:


1. binomische Formel: $(a+b)^{2}=a^{2}+2ab+b^{2}$

2. binomische Formel: $(a-b)^{2}=a^{2}-2ab+b^{2}$

3. binomische Formel: $(a+b)(a-b)=a^{2}-b^{2}$

Diese Formeln werden dir im Laufe deiner Schulzeit immer wieder begegnen, weshalb du sie unbedingt auswendig können solltest. Falls dir dies schwer fällt, schaue dir folgendes Video dazu an ;) https://www.youtube.com/watch?v=EYbvhWEG6kE

Herleitung der binomischen Formeln

Bei der Herleitung der binomischen Formeln werden die Terme in den Klammern ausmultipliziert.

Übung: Binomische Formeln herleiten

Versuche, die erste binomische Formel in deinem Heft rechnerisch herzuleiten.

Beginne mit dem Ausgangsterm (a+b)² und schreibe die Potenz wiefolgt aus: (a+b)(a+b). Dies kannst du nun nach den bekannten Regeln ausmultiplizieren.

(a+b)² = (a+b)\cdot(a+b) = aa+ab+ba+bb = a²+2ab+b²

Herleitung über Flächen von Quadraten

Aufgabenteil

Aufgabe 1:

...

Aufgabe 2:

...

Aufgabe 3:

...