Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 97: Zeile 97:
{{Lösung versteckt|1= Damit die Gerade <math>g</math> in der Ebene <math>E</math> liegt, muss der Richtungsvektor von <math>g</math> und der Normalenvektor von <math>E</math> orthogonal zueinander sein. |2=Tipp 1 anzeigen|3=Tipp 1 verbergen}}
{{Lösung versteckt|1= Damit die Gerade <math>g</math> in der Ebene <math>E</math> liegt, muss der Richtungsvektor von <math>g</math> und der Normalenvektor von <math>E</math> orthogonal zueinander sein. |2=Tipp 1 anzeigen|3=Tipp 1 verbergen}}
{{Lösung versteckt|1= Wenn die Gerade <math>g</math> in der Ebene <math>E</math> liegt, liegt jeder Punkt auf der Gerade <math>g</math> auch in der Ebene <math>E</math>. Prüfe mit der Punktprobe, ob der Stützvektor von <math>g</math> in der Ebene  <math>E</math> liegt.|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}}
{{Lösung versteckt|1= Wenn die Gerade <math>g</math> in der Ebene <math>E</math> liegt, liegt jeder Punkt auf der Gerade <math>g</math> auch in der Ebene <math>E</math>. Prüfe mit der Punktprobe, ob der Stützvektor von <math>g</math> in der Ebene  <math>E</math> liegt.|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}}
{{Lösung versteckt|1= Finde zuerst m: <math> \vec{u} \circ \vec{n} = \left( \begin{matrix} 3\\ m\\ 3,6 \end{matrix} \right) \circ \left( \begin{matrix} -2\\ 3\\ -1 \end{matrix} \right) = 3m - 9,6 </math>. Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt <math> 0 </math> sein: <math> 3m - 9,6 = 0 \Rightarrow m = 3,2 </math>.
{{Lösung versteckt|1= '''Finde zuerst m:''' <math> \vec{u} \circ \vec{n} = \left( \begin{matrix} 3\\ m\\ 3,6 \end{matrix} \right) \circ \left( \begin{matrix} -2\\ 3\\ -1 \end{matrix} \right) = 3m - 9,6 </math>.  
Finde danach l durch eine Punktprobe:  Setze <math> \vec(a) = \left( \begin{matrix} l\\ 5,1\\ 0,4 \end{matrix} \right) </math> in die Ebenengleichung ein und löse nach l auf: <math> -2l + 3 \cdot 5,1 - 0,4 = 3 \Leftrightarrow l = 5,95</math>.  |2=Lösung anzeigen|3=Lösung verbergen}}
Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt <math> 0 </math> sein: <math> 3m - 9,6 = 0 \Rightarrow m = 3,2 </math>.
 
'''Finde danach l durch eine Punktprobe:''' Setze <math> \vec(a) = \left( \begin{matrix} l\\ 5,1\\ 0,4 \end{matrix} \right) </math> in die Ebenengleichung ein und löse nach l auf: <math> -2l + 3 \cdot 5,1 - 0,4 = 3 \Leftrightarrow l = 5,95</math>.  |2=Lösung anzeigen|3=Lösung verbergen}}


c) Die Gerade <math> i: \vec{x} = \left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} -3\\ 5\\ -1 \end{matrix} \right) </math> soll die Ebene <math> E </math> schneiden.
c) Die Gerade <math> i: \vec{x} = \left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} -3\\ 5\\ -1 \end{matrix} \right) </math> soll die Ebene <math> E </math> schneiden.
|Arbeitsmethode}}
|Arbeitsmethode}}


{{Lösung versteckt|1=Es gibt keine eindeutige Lösung! Der Richtungsvektor <math> \vec{u} </math> von <math>g</math> darf nur nicht orthogonal zum Normalenvektor von <math>E</math> liegen. |2=Tipp anzeigen|3=Tipp verbergen}}
{{Lösung versteckt|1= Für <math> m = 3 </math> ist der Richtungsvektor von <math>g</math> orthogonal zum Normalenvektor von <math>E</math> und die Gerade <math>g</math> liegt parallel zur Ebene <math>E</math>. Jeder andere Wert für <math>m</math> ist eine richtige Lösung. |2=Lösung anzeigen|3=Lösung verbergen}}


===&#x2B50;Berechnung des Winkels zwischen Gerade und Ebene===
===&#x2B50;Berechnung des Winkels zwischen Gerade und Ebene===

Version vom 6. Mai 2021, 14:20 Uhr

Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".

Bauarbeiter.jpg



Info

In diesem Lernpfadkapitel <Kurzbeschreibung des Kapitelziels>

Bei den Aufgaben unterscheiden wir folgende Typen:

  • In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
  • Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
  • Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
  • Aufgaben und Kapitel, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.
Viel Erfolg!

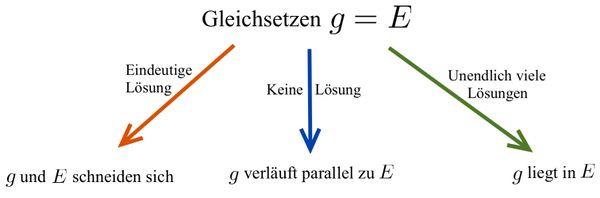
Lagebeziehung Gerade-Ebene


Mögliche Lagebeziehungen zwischen Gerade und Ebene

Aufgabe: Lückentext zur Lagebeziehung zwischen Gerade und Ebene



Merke: Lagebeziehung von Gerade und Ebene untersuchen mit Ebene in Parameterform.
Vorgehen Lagebeziehung Gerade und Ebene.jpg


Beispielaufgabe: Untersuchung der Lagebeziehung von Gerade und Ebene


Gegeben sind eine Ebene und eine Gerade . Untersuche die Lagebeziehung der Gerade und der Ebene und bestimme gegebenenfalls den Schnittpunkt.


1. Schritt: Setze die Geraden- und Ebenengleichung gleich.


2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf.


3. Schritt: Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner.


4. Schritt: Interpretiere die Lösung des Gleichungssystems anhand der Anzahl der Lösungen. Da das Gleichungssystem nur eine Lösung hat, besitzen die Ebene und die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} nur einen gemeinsamen Punkt. Also schneidet die Gerade die Ebene.


5. Schritt: Da sich die Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} und die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} schneiden, kannst du den Schnittpunkt der beiden berechnen. Setze dafür den Parameter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r} in die Geradengleichung ein. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g: \left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + 1 \cdot \left( \begin{matrix} -1\\ -4\\ 0 \end{matrix} \right) = \left( \begin{matrix} 1\\ -2\\ 2 \end{matrix} \right) }


Aufgabe: Untersuchung der Lagebeziehung zwischen Gerade und Ebene

Gegeben ist eine Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E: \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) } .



1. Setze die Geradengleichung mit der Ebenengleichung gleich.

2. Stelle ein LGS auf.

3. Löse das LGS mit dem Gaußverfahren oder dem Taschenrechner.

4. Die Anzahl der Lösungen zeigt dir, wie viele gemeinsamen Punkte die Gerade und die Ebene haben. Daran kannst du die Lagebeziehung erkennen.


⭐Merke: Lagebeziehung von Gerade und Ebene untersuchen mit Ebene in Koordinatenform.
Vorgehen Lagebeziehung Gerade und Ebene1.jpg


Beispiel: Lagebeziehung einer Gerade und einer Ebene in Koordinatenform

Gegeben sind eine Ebene und eine Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g: \vec{x}=\left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -3\\ 5\\ -1 \end{matrix} \right) } . Bestimme die Lagebeziehung von Gerade und Ebene.

1. Prüfe, ob der Richtungsvektor der Gerade orthogonal zum Normalenvektor der Ebene liegt: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{n} \circ \vec{u} = \left( \begin{matrix} 2\\ 1\\ -1 \end{matrix} \right) \circ \left( \begin{matrix} -3\\ 5\\ -1 \end{matrix} \right) = 2 \cdot (-3) + 1 \cdot 5 -1 \cdot (-1) = 0 \Rightarrow \vec{n} \perp \vec{u}}

2. Prüfe durch eine Punktprobe, ob der Stützvektor der Gerade in der Ebene liegt: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 2 \cdot 3 -2 =5 \Rightarrow 4 = 5 \Rightarrow } Der Stützvektor liegt nicht in der Ebene. Daher verlaufen die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g } und die Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} parallel zueinander.


Aufgabe: Bestimme den Parameter

Gegeben ist eine Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E: \vec{x} = -2x_1 + 3x_2 - x_3 = 3 } . Bestimme und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle m } in den folgenden Geraden so, dass die entsprechende Lagebeziehung erfüllt ist.

a) Die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g: \vec{x} = \left( \begin{matrix} 5\\ 3\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} 0,5\\ 3\\ m \end{matrix} \right) } soll parallel zur Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E } verlaufen.

Damit die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} und die Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} parallel zueinander sind, müssen der Richtungsvektor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} und der Normalenvektor von orthogonal zueinander sein.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{u} \circ \vec{n} = \left( \begin{matrix} 0,5\\ 3\\ m \end{matrix} \right) \circ \left( \begin{matrix} -2\\ 3\\ -1 \end{matrix} \right) = 8-m } .

Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0 } sein: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 8-m = 0 \Rightarrow m = 8 } .

b) Die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h: \vec{x} = \left( \begin{matrix} l\\ 5,1\\ 0,4 \end{matrix} \right) + s \cdot \left( \begin{matrix} 3\\ m\\ 3,6 \end{matrix} \right) } soll in der Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E } liegen.

Damit die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} in der Ebene liegt, muss der Richtungsvektor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} und der Normalenvektor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} orthogonal zueinander sein.
Wenn die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} in der Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} liegt, liegt jeder Punkt auf der Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} auch in der Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} . Prüfe mit der Punktprobe, ob der Stützvektor von in der Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} liegt.

Finde zuerst m: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{u} \circ \vec{n} = \left( \begin{matrix} 3\\ m\\ 3,6 \end{matrix} \right) \circ \left( \begin{matrix} -2\\ 3\\ -1 \end{matrix} \right) = 3m - 9,6 } . Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0 } sein: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 3m - 9,6 = 0 \Rightarrow m = 3,2 } .

Finde danach l durch eine Punktprobe: Setze Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec(a) = \left( \begin{matrix} l\\ 5,1\\ 0,4 \end{matrix} \right) } in die Ebenengleichung ein und löse nach l auf: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle -2l + 3 \cdot 5,1 - 0,4 = 3 \Leftrightarrow l = 5,95} .

c) Die Gerade soll die Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E } schneiden.

Es gibt keine eindeutige Lösung! Der Richtungsvektor Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{u} } von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} darf nur nicht orthogonal zum Normalenvektor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} liegen.
Für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle m = 3 } ist der Richtungsvektor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} orthogonal zum Normalenvektor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} und die Gerade liegt parallel zur Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} . Jeder andere Wert für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle m} ist eine richtige Lösung.

⭐Berechnung des Winkels zwischen Gerade und Ebene

Abbildung: Winkel zwischen Gerade und Ebene


Erläuterung: Winkel berechnen zwischen Gerade und Ebene
Wenn eine Gerade g eine Eben E schneidet, kannst du nicht nur den Schnittpunkt berechnen, sondern auch den Schnittwinkel. Dafür benötigen wir den Normalenvektor. Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in Kapitel...


Merksatz: Winkel berechnen zwischen Gerade und Ebene

Sei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} eine Ebene mit dem Normalenvektor Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle n} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} eine Gerade mit dem Richtungsvektor Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle u} . Der Schnittwinkel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \beta} zwischen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} kann mit folgender Formel berechnet werden: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle sin(\beta)=\frac{ n \ast u}{|n| \cdot |u|}}


Wenn du wissen möchtest, warum du nicht wie beim Winkel zwischen zwei Geraden den Kosinus benutzt, kannst du das hier nachlesen:

Der Normalenvektor Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{n}} einer Ebene steht in einem 90 Winkel zur Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} . Wenn wir den Winkel zwischen einer Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} und einer Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} berechnen wollen, können wir wie beim Winkel zwischen zwei Geraden mit der Kosinusfunktion den Winkel zwischen dem Richtungsvektor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} und dem Normalenvektor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} berechnen. In Abbildung ... ist dieser Winkel mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \beta} bezeichnet. Um nun den Winkel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha} zwischen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} zu erhalten, müssen wir Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \beta} von 90 abziehen. Dies entspricht der obigen Formel mit der Sinusfunktion.


Beispiel: Berechnen des Winkels zwischen Gerade und Ebene

Gegeben sind die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g: \vec{x}=\left( \begin{matrix} -1\\ 3\\ 6 \end{matrix} \right) + r \cdot \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) } und die Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E: 2x_1 + x_2 + 4 x_3 = -27 } . Bestimme den Winkel unter dem sich die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} und die Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} schneiden.

1. Schritt: Notiere den Richtungvektor Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{u} } der Gerade und den Normalenvektor Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{n} } der Ebene.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{u}= \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) } und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{n}= \left( \begin{matrix} 2\\ 1\\ 4 \end{matrix} \right) } .

2. Schritt: Setze die Vektoren in die Formel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle sin(\beta)=\frac{ \vec{n} \ast \vec{u}}{|\vec{n}| \cdot |\vec{u}|}} ein. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle sin(\beta)=\frac{ | \left( \begin{matrix} 2\\ 1\\ 4 \end{matrix} \right) \ast \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right)|}{|\left( \begin{matrix} 2\\ 1\\ 4 \end{matrix} \right)| \cdot | \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right)|} \Leftrightarrow sin(\beta)=\frac{18}{\sqrt{60} \cdot \sqrt{21}} \Leftrightarrow sin(\beta)=\frac{18}{\sqrt{1260}} }

3. Schritt: Umformen der Gleichung

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \beta = sin^{-1}(\frac{18}{\sqrt{1260}}) \Leftrightarrow \beta \approx 28,45 }


Aufgabe <Nummer>: <Name>
Inhalt


Aufgabe <Nummer>: Gerade gesucht


Eine Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} soll die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_1-x_2-Ebene } in einem Winkel von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 45} schneiden. Über die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} ist nur bekannt, dass sie im Punkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle P (1|2|3) } beginnt und sie in Richtung des Vektors Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{x}=\left( \begin{matrix} 3\\ 6\\ z \end{matrix} \right)} verläuft. Stelle die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} auf.

Inhalt
Inhalt
Inhalt


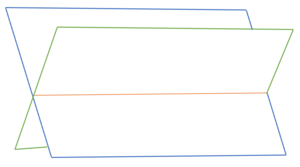
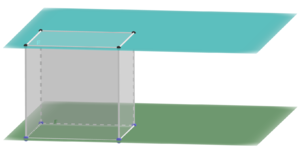
Lagebeziehung Ebene-Ebene

Basiswissen

Aufgabe: Lückentext zur Lagebeziehung zwischen Ebene und Ebene


Schnittgerade von zwei Ebenen.png
Parallele Ebenen.png


Untersuchung der Lagebeziehung zwischen zwei Ebenen

Seien E und F zwei Ebenen im Raum. Um die Lagebeziehung dieser Ebenen zu untersuchen, müssen eine Reihe bestimmter Rechenschritte durchgeführt werden:

Schritt 1: Die beiden Ebenengleichungen gleichsetzen

Schritt 2: LGS interpretieren

Schritt 3: Schnittgerade bestimmen


Aufgabe: Ergebnisse interpretieren

Interpretiere die jeweilige Situation geometrisch.

a) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{vmatrix} 1 & 0 & 0 & -0,5 & 0,5 \\ 0 & 1 & 0 & -1 & 0,5 \\ 0 & 0 & 1 & 1,5 & 1 \end{vmatrix}}

b) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{vmatrix} 1 & 0 & -1 & -2 & 0 \\ 0 & 1 & -1 & -3 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{vmatrix}}

c) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{vmatrix} 1 & 0 & -1 & -2 & 1 \\ 0 & 1 & -1 & -3 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{vmatrix}}


Aufgabe: Lagebeziehungen berechnen

Untersuche die Lagebeziehung der jeweiligen Ebenen.

a) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} }

b) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} }

c) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} }


Aufgabe: Schnitt von zwei Zeltflächen

Die beiden Seitenflächen eines Zeltes liegen in den Ebenen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E: \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}, r,s \in \mathbb{R} } und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E: \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ -3 \\ 4 \end{pmatrix}, t,u \in \mathbb{R} } . Berechne die Geradengleichung der oberen Zeltkante.


⭐Berechnung des Winkels zwischen Ebene und Ebene

Merke: Winkel berechnen zwischen zwei Ebenen

Wenn sich zwei Ebenen schneiden, kann der Schnittwinkel bestimmt werden, den sie einschließen. Wie in Abbildung ... zu sehen ist, kannst du dazu die Normalenvektoren betrachten. Sie schließen denselben Winkel ein, wie die beiden Ebenen. Betrachten wir die Normalenvektoren, so können wir ähnlich vorgehen, wie beim Berechnen des Winkels zwischen zwei Geraden.

Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum


Merksatz: <Name>
Seien Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F} zwei sich schneidende Ebenen mit den Normalenvektoren Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle n} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle m} . Der Schnittwinkel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha} zwischen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F} kann mit folgender Formel berechnet werden: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle cos(\alpha)=\frac{ n \ast m}{|n| \cdot |m|}}


Beispiel: Winkel berechnen zwischen zwei Ebenen
Inhalt


Aufgabe <Nummer>: Fehlerbeschreibung
Inhalt


Aufgabe <Nummer>: Bank am Wanderweg

An einem Wanderweg soll eine Holzbank aufgestellt werden. Die Bank wird so ausgerichtet, dass die Sitzfläche durch die Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle S_1: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0,5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0,4 \\ 0\end{pmatrix}, r,s \in \mathbb{R} } und die Rückenlehne durch die Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R_1: -x_2 + 0,4 x_3 = -0,2 } beschrieben werden kann.

a) Um eine bequeme Sitzposition zu ermöglichen, sollte der Winkel zwischen Rückenlehne und Sitzfläche zwischen 100 und 110 liegen. Überprüfe, ob dies auf die neue Bank zutrifft.

Berechne zunächst den Normalenvektor der Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle S-1 } aus den Richtungsvektoren der Ebene. Wenn du nicht mehr genau weißt, wie das geht, schaue in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum.
Überlege genau, welchen Winkel du berechnet hast. Vielleicht kann dir eine Skizze helfen.

Als Normalenvektor der Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle S_1} erhält man Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{n}=\begin{pmatrix} 0 \\ 0 \\ 0,8 \end{pmatrix} } und als Normalenvektor der Ebene . Einsetzen in die Formel liefert:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle cos(\alpha)=\frac{ | \left( \begin{matrix} 0\\ 0\\ 0,8 \end{matrix} \right) \ast \left( \begin{matrix} 0\\ -1\\ 0,4 \end{matrix} \right)|}{|\left( \begin{matrix} 0\\ 0\\ 0,8 \end{matrix} \right)| \cdot | \left( \begin{matrix} 0\\ -1\\ 0,4 \end{matrix} \right)|} \Leftrightarrow cos(\alpha)=\frac{\frac{8}{25}}{\frac{4}{5} \cdot \sqrt{\frac{29}{25}}} }

Umstellen der Formel ergibt: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha=cos^{-1} \left( \frac{\frac{8}{25}}{\frac{4}{5} \cdot \sqrt{\frac{29}{25}}} \right) \Leftrightarrow \alpha \approx 68,2 ^\circ }

Wie in Abbildung ... zu sehen wurde der Winkel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha } berechnet. Der Winkel zwischen der Sitzfläche und der Rückenlehne wird aber durch den Winkel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \beta } beschrieben. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \beta} erhält man, indem man Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 180 ^\circ - \alpha } berechnet: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 180 ^\circ - 68,2 ^\circ = 111,8 ^\circ } . Mit einem Wert von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 111,8 ^\circ } liegt der Winkel zwischen Rückenlehne und Sitzfläche etwas über dem optimalen Winkel.

b) Da der Wanderweg sehr beliebt ist, soll noch eine zweite Bank aufgestellt werden. Sie wird so ausgerichtet, dass beide Bänke mit den Rückenlehnen aneinander stehen. Auch bei der zweiten Bank können die Sitzfläche und die Rückenlehne durch Ebenen beschrieben werden. Die Sitzfläche entspricht der Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle S_2: \vec{x} = \begin{pmatrix} 0 \\ 0,8 \\ 0,5 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 0,4 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0 \\ 0\end{pmatrix}, r,s \in \mathbb{R}} und die Rückenlehne der Ebene Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R_2: -x_2 - 0,4 x_3 = -1 } Berechne den Winkel, unter dem die beiden Rückenlehnen der Bänke aufeinander treffen.

Inhalt

Es soll der Winkel zwischen den beiden Rückenlehnen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R_1} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R_2} berechnet werden. Die Normalenvektoren der Ebenen lauten Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{m}=\begin{pmatrix} 0 \\ -1 \\ 0,4 \end{pmatrix} } und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{l}=\begin{pmatrix} 0 \\ -1 \\ -0,4 \end{pmatrix} } . Einsetzen in die Formel liefert:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle cos(\alpha)=\frac{ | \left( \begin{matrix} 0\\ -1\\ 0,4 \end{matrix} \right) \ast \left( \begin{matrix} 0\\ -1\\ -0,4 \end{matrix} \right)|}{|\left( \begin{matrix} 0\\ -1\\ 0,4 \end{matrix} \right)| \cdot | \left( \begin{matrix} 0\\ -1\\ -0,4 \end{matrix} \right)|} }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Leftrightarrow cos(\alpha)=\frac{\frac{21}{25}}{\sqrt{\frac{29}{25}} \cdot \sqrt{\frac{29}{25}}} }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Leftrightarrow cos(\alpha)=\frac{\frac{21}{25}}{\frac{29}{25}}} }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Leftrightarrow cos(\alpha)=\frac{21}{29}}

Umstellen der Formel ergibt: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha=cos^{-1} \left( \frac{21}{29} \right) \Leftrightarrow \alpha \approx 43,6 ^\circ } . Der Winkel zwischen den beiden Rückenlehnen beträgt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 43,6 ^\circ } .
Abgerufen von „https://projektwiki.idea-sketch.com/index.php?title=Digitale_Werkzeuge_in_der_Schule/Unterwegs_in_3-D_–_Punkte,_Vektoren,_Geraden_und_Ebenen_im_Raum/Lagebeziehungen_und_Winkel_(Gerade_und_Ebene,_2_Ebenen)&oldid=48975“