Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 21: | Zeile 21: | ||
===Mögliche Lagebeziehungen zwischen Gerade und Ebene=== | ===Mögliche Lagebeziehungen zwischen Gerade und Ebene=== | ||
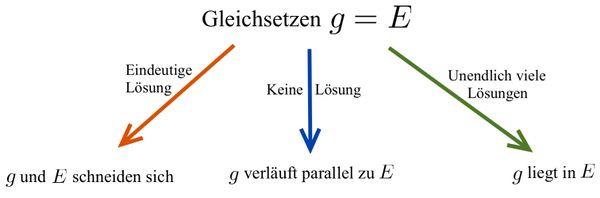
Zwischen einer Gerade und einer Ebene gibt es drei mögliche Lagebeziehungen. | Zwischen einer Gerade und einer Ebene gibt es drei mögliche Lagebeziehungen. | ||
<br />[[Datei:Lagebeziehung_Gerade_Ebene_schneidend.jpg|rahmenlos|332x332px]][[Datei:Lagebeziehung_Gerade_Ebene_parallel.jpg|rahmenlos]][[Datei:Lagebeziehung_Gerade_Ebene_liegtin.jpg|rahmenlos]] | <br />[[Datei:Lagebeziehung_Gerade_Ebene_schneidend.jpg|rahmenlos|332x332px]][[Datei:Lagebeziehung_Gerade_Ebene_parallel.jpg|rahmenlos]][[Datei:Lagebeziehung_Gerade_Ebene_liegtin.jpg|rahmenlos]] | ||
=== Untersuchung der Lagebeziehung zwischen Gerade und Ebene === | |||
{{3Spalten | |||
| | |||
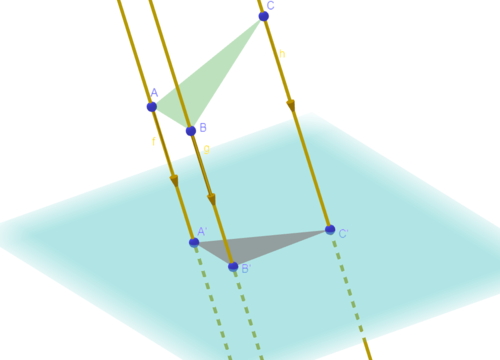
Die Geraden schneidet die Ebene. | |||
| | |||
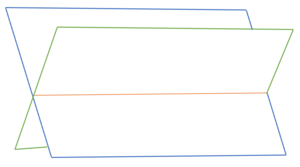
Die Gerade und die Ebene liegen parallel. | |||
| | |||
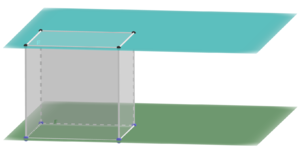
Die Gerade liegt in der Ebene. | |||
}} | |||
===Untersuchung der Lagebeziehung zwischen Gerade und Ebene=== | |||
{{Box|Aufgabe: Lückentext zur Lagebeziehung zwischen Gerade und Ebene| | {{Box|Aufgabe: Lückentext zur Lagebeziehung zwischen Gerade und Ebene| | ||
{{LearningApp|width=100%|height=500px|app=pfhf979bk21}} | {{LearningApp|width=100%|height=500px|app=pfhf979bk21}} | ||
Version vom 7. Mai 2021, 13:14 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
In diesem Lernpfadkapitel <Kurzbeschreibung des Kapitelziels>
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
- Aufgaben und Kapitel, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.
Inhaltsverzeichnis
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Zwischen einer Gerade und einer Ebene gibt es drei mögliche Lagebeziehungen.
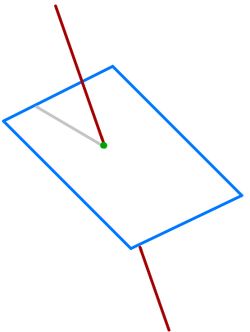
Die Geraden schneidet die Ebene.
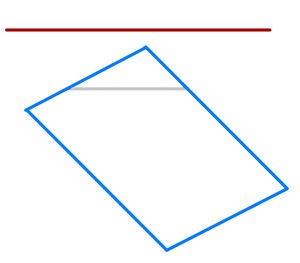
Die Gerade und die Ebene liegen parallel.
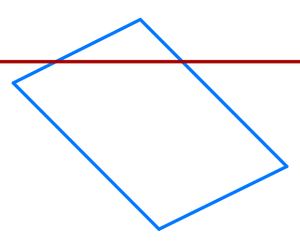
Die Gerade liegt in der Ebene.
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
Gegeben sind eine Ebene 

1. Schritt: Setze die Geraden- und Ebenengleichung gleich. 
2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf. 
3. Schritt: Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner. 
4. Schritt: Interpretiere die Lösung des Gleichungssystems anhand der Anzahl der Lösungen. Da das Gleichungssystem nur eine Lösung hat, besitzen die Ebene 

5. Schritt: Da sich die Ebene 



Gegeben ist eine Ebene 
1. Setze die Geradengleichung mit der Ebenengleichung gleich.
2. Stelle ein LGS auf.
3. Löse das LGS mit dem Gaußverfahren oder dem Taschenrechner.
4. Die Anzahl der Lösungen zeigt dir, wie viele gemeinsamen Punkte die Gerade und die Ebene haben. Daran kannst du die Lagebeziehung erkennen.
Da es Frau Meier im Sommer auf ihrer Terrasse gerne schattig haben möchte, spannt sie ein dreieckiges Segeltuch auf. Die Eckpunkte des Segeltuchs sind </nowiki>



 -Ebene und du weißt, dass jeder Punkt auf dieser Ebene von der Form:
-Ebene und du weißt, dass jeder Punkt auf dieser Ebene von der Form:  ist. Du musst also die Ebenengleichung nicht aufstellen.
ist. Du musst also die Ebenengleichung nicht aufstellen.
Gegeben sind eine Ebene 

1. Prüfe, ob der Richtungsvektor der Gerade orthogonal zum Normalenvektor der Ebene liegt: Fehler beim Parsen (Syntaxfehler): {\displaystyle \vec{n} \circ \vec{u} = \left( \begin{matrix} 2\\ 1\\ -1 \end{matrix} \right) \circ \left( \begin{matrix} -3\\ 5\\ -1 \end{matrix} \right) = 2 \cdot (-3) + 1 \cdot 5 -1 \cdot (-1) = 0 \Rightarrow \vec{n} \perp \vec{u}}
2. Prüfe durch eine Punktprobe, ob der Stützvektor der Gerade in der Ebene liegt: 


Gegeben ist eine Ebene 


a) Die Gerade 

 und die Ebene
und die Ebene  parallel zueinander sind, müssen der Richtungsvektor von
parallel zueinander sind, müssen der Richtungsvektor von  und der Normalenvektor von
und der Normalenvektor von  orthogonal zueinander sein.
orthogonal zueinander sein.
 sein:
sein:  .
.b) Die Gerade 

 in der Ebene
in der Ebene  liegt, muss der Richtungsvektor von
liegt, muss der Richtungsvektor von  und der Normalenvektor von
und der Normalenvektor von  orthogonal zueinander sein.
orthogonal zueinander sein. in der Ebene
in der Ebene  liegt, liegt jeder Punkt auf der Gerade
liegt, liegt jeder Punkt auf der Gerade  auch in der Ebene
auch in der Ebene  . Prüfe mit der Punktprobe, ob der Stützvektor von
. Prüfe mit der Punktprobe, ob der Stützvektor von  in der Ebene
in der Ebene  liegt.
liegt.Finde zuerst m: 


 durch eine Punktprobe: Setze
durch eine Punktprobe: Setze  in die Ebenengleichung ein und löse nach l auf:
in die Ebenengleichung ein und löse nach l auf:  .
.c) Die Gerade 

 von
von  darf nur nicht orthogonal zum Normalenvektor von
darf nur nicht orthogonal zum Normalenvektor von  liegen.
liegen. ist der Richtungsvektor von
ist der Richtungsvektor von  orthogonal zum Normalenvektor von
orthogonal zum Normalenvektor von  und die Gerade
und die Gerade  liegt parallel zur Ebene
liegt parallel zur Ebene  . Jeder andere Wert für
. Jeder andere Wert für  ist eine richtige Lösung.
ist eine richtige Lösung.
Luca hält einen Vortrag vor seiner Klasse. Mit einem Laserpointer möchte er auf einer Karte an der Wand etwas zeigen. Die Wand des Klassenraums wird durch die Ebene 



⭐Berechnung des Winkels zwischen Gerade und Ebene
Sei 







Wenn du wissen möchtest, warum du nicht wie beim Winkel zwischen zwei Geraden den Kosinus benutzt, kannst du das hier nachlesen:
 einer Ebene steht in einem 90 Winkel zur Ebene
einer Ebene steht in einem 90 Winkel zur Ebene  . Wenn wir den Winkel zwischen einer Gerade
. Wenn wir den Winkel zwischen einer Gerade  und einer
und einer  berechnen wollen, können wir wie beim Winkel zwischen zwei Geraden mit der Kosinusfunktion den Winkel zwischen dem Richtungsvektor von
berechnen wollen, können wir wie beim Winkel zwischen zwei Geraden mit der Kosinusfunktion den Winkel zwischen dem Richtungsvektor von  und dem Normalenvektor von
und dem Normalenvektor von  berechnen. In Abbildung ... ist dieser Winkel mit
berechnen. In Abbildung ... ist dieser Winkel mit  bezeichnet. Um nun den Winkel
bezeichnet. Um nun den Winkel  zwischen
zwischen  und
und  zu erhalten, müssen wir
zu erhalten, müssen wir  von
von  abziehen. Dies entspricht der obigen Formel mit der Sinusfunktion.
abziehen. Dies entspricht der obigen Formel mit der Sinusfunktion.
Gegeben sind die Gerade 



1. Schritt: Notiere den Richtungvektor 



2. Schritt: Setze die Vektoren in die Formel 

3. Schritt: Umformen der Gleichung

Eine Gerade 






 -Ebene verläuft nur in
-Ebene verläuft nur in  -Richtung.
-Richtung.Bisher wurde mit der Formel zu Winkelberechnung nur der Winkel berechnet. Die Formel kann jedoch auch genutzt werden, um bei einem vorgegebenen Winkel die Lage der Gerade oder Ebene zu bestimmen.
Dafür muss zuerst der Normalenvektor der Ebene bestimmt werden. Da es sich um die 

Nun können der Normalenvektor der Ebene, der Richtungsvektor der Gerade und der vorgegebene Winkel in die Formel zur Berechnung eingesetzt werden: 
Löst man die Gleichung mithilfe des Taschenrechners, erhält man das Ergebnis: 
 aufgestellt werden. Man erhält
aufgestellt werden. Man erhält  .
.
Lagebeziehung Ebene-Ebene
Gegeben sind eine Ebene 

1. Schritt: Setze die beiden Ebenengleichungen gleich. 
2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf. 
Interpretiere die jeweilige Situation geometrisch.
a) 
b) 
c) 
Untersuche die Lagebeziehung der jeweiligen Ebenen.
a) 
b) 
c) 
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen 

⭐Berechnung des Winkels zwischen Ebene und Ebene
Wenn sich zwei Ebenen schneiden, kann der Schnittwinkel bestimmt werden, den sie einschließen. Wie in Abbildung ... zu sehen ist, kannst du dazu die Normalenvektoren betrachten. Sie schließen denselben Winkel ein, wie die beiden Ebenen. Betrachten wir die Normalenvektoren, so können wir ähnlich vorgehen, wie beim Berechnen des Winkels zwischen zwei Geraden.
Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum
 und
und  zwei sich schneidende Ebenen mit den Normalenvektoren Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle n}
und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle m}
. Der Schnittwinkel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha}
zwischen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E}
und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F}
kann mit folgender Formel berechnet werden: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle cos(\alpha)=\frac{ \vec{n} \ast \vec{m}}{|\vec{n}| \cdot |\vec{m}|}}
zwei sich schneidende Ebenen mit den Normalenvektoren Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle n}
und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle m}
. Der Schnittwinkel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha}
zwischen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E}
und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F}
kann mit folgender Formel berechnet werden: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle cos(\alpha)=\frac{ \vec{n} \ast \vec{m}}{|\vec{n}| \cdot |\vec{m}|}}
Gegeben sind zwei Ebenen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E}
und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F}
mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E: \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 3 \\ -6 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 1 \\ 0\end{pmatrix}, r,s \in \mathbb{R}}
und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F: 7x_1+x_2-3x_3 }
. Berechne den Schnittpunkt zwischen den Ebenen.
1. Schritt: Bestimmte die Normalenvektoren von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F} .
Der Normalenvektor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} kann mithilfe des ... bestimmt werden als Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{n} = \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} } . Der Normalenvektor von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F} lautet Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{m} = \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix} } .
2. Schritt: Einsetzen der Normalenvektoren in die Formel.
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle cos(\alpha) = \frac{ \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \ast \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}}{\begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \cdot \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}} \Leftrightarrow cos(\alpha) = \frac{59}{\sqrt{9} \cdot \sqrt{59}} \Leftrightarrow cos(\alpha) = \frac{16}{3 \cdot \sqrt{59}}}
3. Schritt: Auflösen der Gleichung.
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha = cos^{-1}(\frac{16}{3 \cdot \sqrt {59}}) \Leftrightarrow \alpha \approx 46{,}03 ^{\circ}} Der Winkel zwischen den Ebenen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle E} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F} beträgt ca. .
.
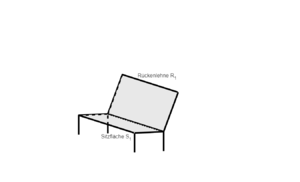
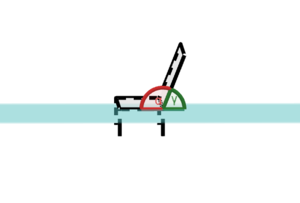
An einem Wanderweg soll eine Holzbank aufgestellt werden. Die Bank wird so ausgerichtet, dass die Sitzfläche durch die Ebene 

a) Um eine bequeme Sitzposition zu ermöglichen, sollte der Winkel zwischen Rückenlehne und Sitzfläche zwischen 100 und 110 liegen. Überprüfe, ob die auf die neue Bank zutrifft.
 aus den Richtungsvektoren der Ebene. Wenn du nicht mehr genau weißt, wie das geht, schaue in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum.
aus den Richtungsvektoren der Ebene. Wenn du nicht mehr genau weißt, wie das geht, schaue in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum. Als Normalenvektor der Ebene 


Einsetzen in die Formel liefert:

Umstellen der Formel ergibt: 
 berechnet. Der Winkel zwischen der Sitzfläche und der Rückenlehne wird aber durch den Winkel
berechnet. Der Winkel zwischen der Sitzfläche und der Rückenlehne wird aber durch den Winkel  beschrieben.
beschrieben.  erhält man, indem man
erhält man, indem man  berechnet:
berechnet:  . Mit einem Wert von
. Mit einem Wert von  liegt der Winkel zwischen Rückenlehne und Sitzfläche etwas über dem optimalen Winkel.
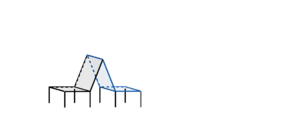
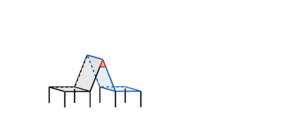
liegt der Winkel zwischen Rückenlehne und Sitzfläche etwas über dem optimalen Winkel.b) Da der Wanderweg sehr beliebt ist, soll noch eine zweite Bank aufgestellt werden. Sie wird so ausgerichtet, dass beide Bänke mit den Rückenlehnen aneinander stehen. Auch bei der zweiten Bank können die Sitzfläche und die Rückenlehne durch Ebenen beschrieben werden. Die Sitzfläche entspricht der Ebene 

 und der Ebene
und der Ebene  . Nutze zur Berechnung die Normalenvektoren der Ebenen.
. Nutze zur Berechnung die Normalenvektoren der Ebenen.