Benutzer:Buss-Haskert/Exponentialfunktion/exponentielles Wachstum

zurück zur Seite der Herta-Lebenstein-Realschule

SEITE IM AUFBAU

Vorwissen
1) Lineares und exponentielles Wachstum (Einstieg)
2) Wachstumsrate und Wachstumsfaktor
3) Exponentielles Wachstum

3 Exponentielles Wachstum

Einstieg: Weltbevölkerung

Im Jahr 2019 lebten 7,7 Mrd. Menschen auf der Erde. Wissenschaflter prognostizierten in diesem Jahr eine jährliche Zuwachsrate von 1,25%.
Also gilt q=100%+1,25% = 101,25% = 1,0125

Wie viele Menschen leben demnach im Jahr 2030 auf der Erde?

Stelle diese Situation auf verschiedene Arten dar. (Erinnerung: Text (ist gegeben), Wertetabelle, Funktionsgleichung und Funktionsgraph)

Datei:Weltbevölkerung Tipp Wertetabelle.png

Prognose für das Jahr 2030: n = 11
W₁₁ = W₀ ∙ q¹¹
   = 7,70 ∙ 1,025¹¹

   ≈8,83

Exponentielles Wachstum - Exponentialgleichung

Wir sprechen von exponentiellem Wachstum, wenn der Wert einer Größe in gleichen Zeitspannen immer um denselben Prozentsatz p% zunimmt bzw. abnimmt.
Die neue Größe nach n Zeitspannen berechnen wir mit
W_n = W₀ · qⁿ,

wobei q der Wachstumsfaktor ist. q = 1+p% (Zunahmen) bzw.q=1-p%(Abnahme)

Die Gleichung W_n = W₀ · qⁿ heißt Exponentialgleichung, da die Variable n im Exponenten steht.

Anwendungsaufgabe 1: Bevölkerungswachstum (W_n gesucht)

Die Bevölkerung in Indien beträgt zur Zeit 1,38 Milliarden Einwohner (2020). Die jährliche Zunahme beträgt derzeit 0,8%.

Wie viele Einwohner hat Indien im Jahr 2025?

geg: W₀ = 1,38 Mrd.; p% = 0,8% = 0,008, also ist q = 1+0,008 = 1,008; n = 5 (von 2020 - 2025)
ges: W₅

W_n = W₀ · qⁿ
W₅ = 1,38 · 1,008⁵
     = 1,436

Indien wird im Jahr 2025 ca. 1,436 Mrd. Einwohner haben.

Exponentialgleichung - Formel umstellen

Anwendungsaufgabe 2: Klimawandel (W₀ gesucht)

Im Jahr 2021 ist die Fläche der Arktis mit 4,7 Mio km² deutlich kleiner als noch vor rund 30 Jahren. Die Abnahme beträgt mit leichten Schwankungen jährlich ca. 1,7%.

Wie groß war die Fläche vor 30 Jahren?

geg: W₃₀ = 4,7 Mio km²; p% = -1,7% = -0,017, also ist q = 1-0,017 = 0,983; n = 30
ges: W₀

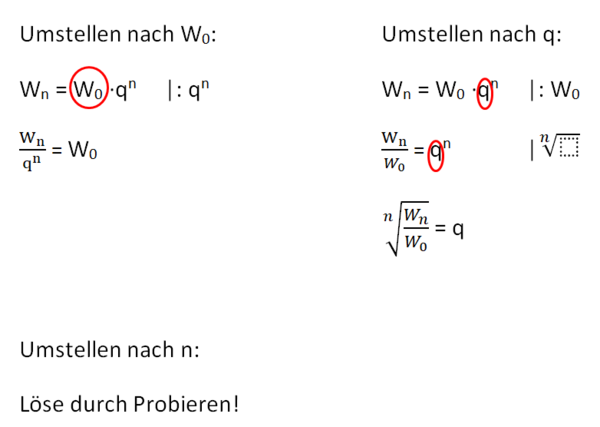
W_n = W₀ · qⁿ   | : qⁿ
W₀ = ${\tfrac {W_{n}}{q^{n}}}$
W₀ = ${\tfrac {W_{30}}{q^{30}}}$
      = ${\tfrac {4,7}{0,983^{30}}}$
     ≈ 7,86

Vor 30 Jahren betrug die Fläche der Arktis noch ca. 7,86 Mio km².

Anwendungsaufgabe 3: Mietpreissteigerung (q und p% gesucht)

Die Miete für eine Wohnung stieg innerhalb von 5 Jahren von 600€ auf 730€.

Um wie viel Prozent ist die Miete durchschnittlich pro Jahr gestiegen?

geg: W₀ = 600 €; W₅ = 730 €; n = 5
ges: q bzw. p%

W_n = W₀ · qⁿ   | : W₀
${\tfrac {W_{n}}{W_{0}}}$ = qⁿ   | ${\sqrt[{n}]{}}$
${\sqrt[{n}]{\tfrac {W_{n}}{W_{0}}}}$W₀ = q
${\sqrt[{5}]{\tfrac {730}{600}}}=q$
1,04 ≈ q
p% = q - 1 = 0,04 = 4%

Die Mietsteigerung betrug jährlich 4%.

Anwendungsaufgabe 4: Temperaturabnahme (n gesucht)

Eine Tasse Tee wird mit kochendem Wasser (100°C) aufgegossen. Die Temperatur sinkt jede Minute um 5%. Es wird empfohlen, Getränke nicht heißer als 65° zu trinken.
Nach wie vielen Minuten ist der Tee kalt genug?

geg: W₀ = 100°; W_n = 65°C ; p% = -5% = -0,05, also q = 1-0,05 = 0,95
ges: n

W_n = W₀ · qⁿ   | Löse durch systematisches Probieren (Wertetabelle)
Für n = 1 gilt:
W₁ = W₀ · q¹   |     = 100 · 0,95¹
    = 95 (°C)
...
Für n = 8 gilt: W₈ = W₀ · q⁸   |     = 100 · 0,95⁸
    ≈ 66,3 (°C)
Für n = 9 gilt: W₉ = W₀ · q⁹   |     = 100 · 0,95⁹
    ≈ 63,0 (°C)

Nach ca. 9 Minuten ist der Tee auf unter 65°C abgekühlt.

ÜBUNGSAUFGABEN ERGÄNZEN

• Formel umstellen
• Verdopplungszeit (Bakterien)

Applet von Hegius, R. Schürz

• Halbwertszeit (Atome)

Applet von Hegius, R. Schürz

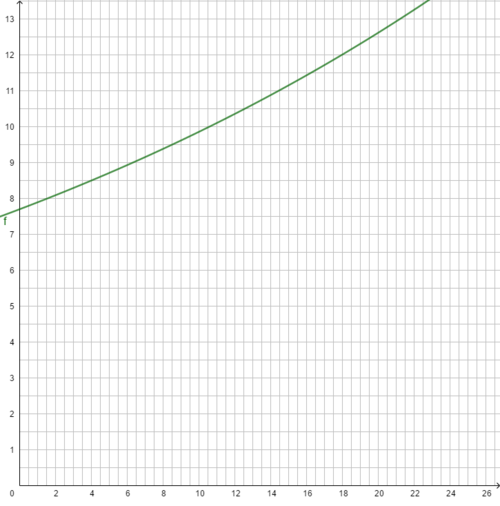
4 Die Exponentialfunktion

Exponentialfunktion

Die Funktion mit der Gleichung f(x) = c∙ax heißt Exponentialfunktion.

Eigenschaften der Exponentialfunktion

Beschreibe die Eigenschaften der Exponentialfunktion f(x) = c∙ax .

Wähle zunächst c=1. Wie verläuft der Graph der Funktion? Löse den Lückentext und übertrage ihn in dein Heft.

Applet von Ralf Wagner

Der Graph verläuft immer oberhalb der x-Achse.
Der Graph geht immer durch den Punkt (0|1).
Für a>1 steigt der Graph (Zunahme),

für 0<a<1 fällt der Graph (Abnahme).