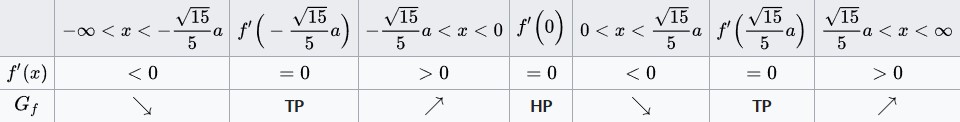Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Monotonie

Merke

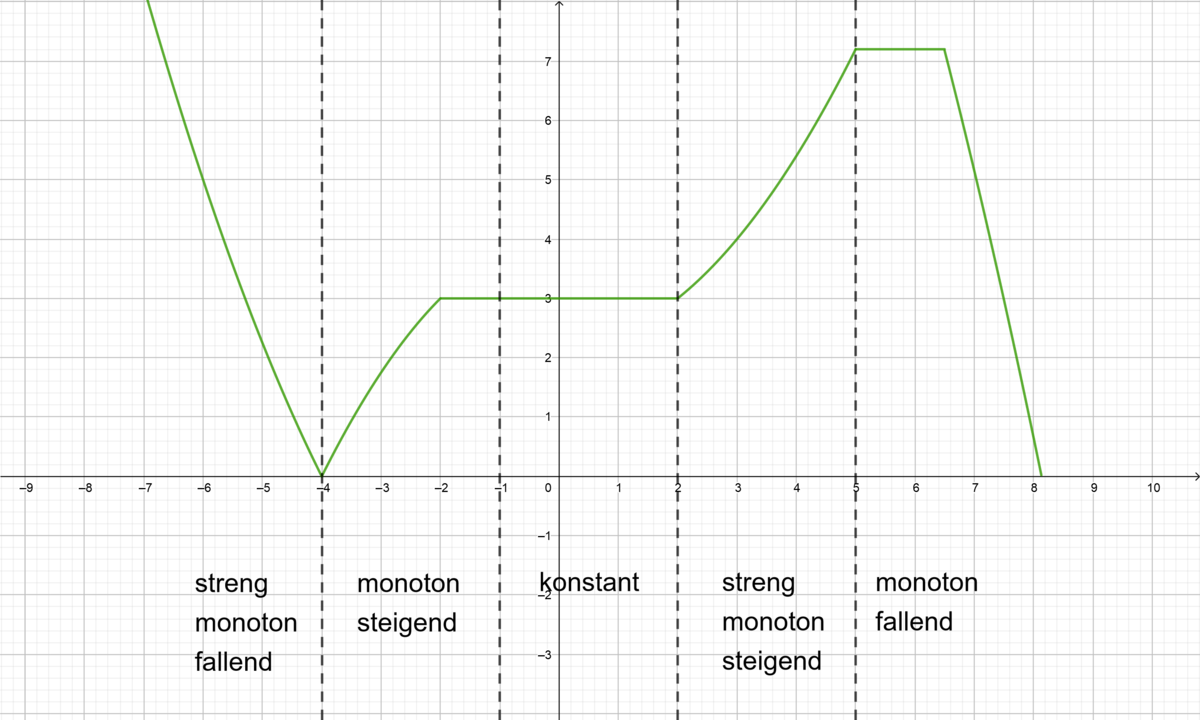
Das Monotonieverhalten einer Funktion beschreibt den Verlauf des Graphen einer Funktion. Die Monotonie gibt an, ob eine Funktion fällt, steigt oder konstant ist.

Sei $h(x)$ eine Funktion und $x_{1}<x_{2}$

-      Falls auf einem Intervall $h(x_{1})<f(x_{2})$ gilt, so ist die Funktion streng monoton steigend

-      Falls auf einem Intervall $h(x_{1})\leq \ f(x_{2})$ gilt, so ist die Funktion monoton steigend

-      Falls auf einem Intervall $h(x_{1})>f(x_{2})$ gilt, so ist die Funktion streng monoton fallend

-      Falls auf einem Intervall $h(x_{1})\geq \ f(x_{2})$ gilt, so ist die Funktion monoton fallend

Wie die einzelnen Eigenschaften am Graphen aussehen, kannst du hier nochmal in der Abbildung sehen!

Aufgabe 1: Zuordnung von Begriffen zur Monotonie

So berechnest du das Monotonieverhalten einer Funktion

1. Erste Ableitung berechnen

2. Nullstellen der ersten Ableitung berechnen

3. Intervalle benennen

4. Monotonietabelle aufstellen

5. Vorzeichen der Intervalle berechnen (z.B. mit Taschenrechner)

6. Ergebnis interpretieren

Beispiel: Monotonieverhalten für $f(x)=x^{2}$ bestimmen

Zuerst berechnen wir die Ableitung $f'(x)=2x$. Anschließend berechnen wir die Nullstellen der Ableitung ($f'(x)=0$) und erhalten durch Umformungen als Nullstelle $x=0$. Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten $]-\infty ,0[$ und $]0,+\infty [$. Darauffolgend berechnen wir die Vorzeichen für die Intervalle. Dies machen wir indem wir Werte für die Ableitung in den entsprechenden Intervallen ausrechnen. Zum Beispiel liegt $-2$ im Intervall $]-\infty ,0[$ $f'(-2)=-4<0$. Die entsprechenden Werte kannst du in einer Tabelle übersichtlich darstellen:

(Legende: $\nearrow {\widehat {=}}$ streng monoton steigend, $\searrow {\widehat {=}}$ streng monoton fallend)

Aus dem Ergebnis können wir schließen, dass die Funktion für $]-\infty ,0[$ streng monoton fallend und für $]0,+\infty [$ streng monoton steigend ist.

Aufgabe 2: Regenschauer am Aasee

Aasee Münster

Nach einem starken Regenschauer in Münster steigt der Wasserspiegel im Aasee an. Die Funktion $g(x)={\frac {1}{4}}x^{3}-{\frac {25}{2}}x^{2}+144x$ beschreibt die Zuflussgeschwindigkeit in den ersten 48 Stunden ($x{\widehat {=}}$ Zeit in Stunden, $g(x){\widehat {=}}$ Zuflussgeschwindigkeit in Liter pro Stunde). Wann fließt innerhalb dieser Zeit Wasser zu und wann Wasser ab?

Stelle dir vor, wie sich der Graph verändert, wenn Wasser zu- bzw. abfließt

Der Graph steigt monton, wenn Wasser dazufließt und fällt monoton, wenn Wasser abfließt. Also musst du die Monotonie der Funktion $g(x)$ berechnen!

Die Monotonie zeigt uns an, wo der Graph steigt und fällt. In dem Sachzusammenhang somit wann der Wasserspiegel zu und auch abnimmt.

Wir berechnen zuerst die Nullstellen der ersten Ableitung:

$g(x)={\frac {1}{4}}x^{3}-{\frac {25}{2}}x^{2}+144x$

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g'(x)=\frac{3}{4}x^{2} -25x +144}

Durch Umformungen erhalten wir die möglichen Extremstellen:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{3}{4}x^{2}-25x+144 =0\;\;\;\;\;\;\;\;|:\frac{3}{4}}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \;x^{2}-\frac{100}{3}x+192 = 0\;\;\;\;\;\;\;\,|} PQ-Formel anwenden

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1/2} = -\frac{p}{2}\pm \sqrt{\Big(\frac{p}{2}\Big)^{2}-q}}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= -\frac{-100}{3}\pm \sqrt{\Big(\frac{-100}{3}\Big)^{2}-\Big(192\Big)}}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Rightarrow x_{1} = 25{,}92} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_{2} = 7{,}40}

Mithilfe der errechneten Intervalle können wir nun die Monotonietabelle aufstellen:

Antwort: Somit fließt Wasser steigt der Wasserspiegel bis zur Stunde 7,4 (seit Messung). Danach fließt es ca. bis zur 26. Stunde ab.

Aufgabe 3: Der"SuperBounce"-Ball ⭐

SuperBounce-Ball

Die Firma "SuperBounce" hat einen speziellen Ball erfunden, der eine einzigartige Sprungbewegung beim Wurf auf dem Boden erzeugt. Die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f_a(x)=\frac{5}{6}x^{4}-a^{2}x^{2}} beschreibt annähernd die Flugbahn des Balles, wobei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a\in[-3,3]} die Härte des Wurfes durch den Werfer beschreibt (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x=} horizontaler Verlauf des Balles in cm, Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f_a(x)\widehat{=}} Höhe des Balles in cm). Bestimme wann der Ball in Abhängikeit von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a} nach oben springt und wann er fällt.

Überlege, wie sich das sprunghafte Verhalten des Balles im Graphen erkennen lässt.

Um zu berechnen, wann der Ball springt und wann er fällt, berechnen wir das Monotonieverhalten der Funktion.

Wir berechnen zuerst die Nullstellen der ersten Ableitung:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f_a(x)=\frac{5}{6}x^{4}-a^{2}x^{2} }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f_a'(x)=\frac{20}{6}x^{3}-2a^{2}x}

Durch Umformungen erhalten wir die möglichen Extremstellen:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \;\;\;\;\;\;\frac{20}{6}x^{3}-2a^{2}x =0\;\;\;\;\;\;\;|} Ausklammern

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \;x\cdot(\frac{20}{6}x^{2}-2a^{2})=0\;\;\;\;\;\;\;|} Satz vom Nullprodukt

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow x_{1} = 0}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle oder\;\;\;\;\;\;\ \frac{20}{6}x^{2} - 2a^{2} = 0\;\;\;\;\;\;\,\;|+2a^{2}}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \frac{20}{6}x^{2}= 2a^{2}\;\;\;\;|:\frac{20}{6}}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \;\;\;\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x^{2} = \frac{3}{5}a^{2}\;|\sqrt{(...)}}

.Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Rightarrow x_{1} = 0, x_{2} = \frac{\sqrt{15}}{5}a, } und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_{3} =-\frac{\sqrt{15}}{5}a }

Mithilfe der errechneten Intervalle können wir nun die Monotonietabelle aufstellen:

Aufgabe 4: Monotonieverhalten anhand der Ableitungsfunktion bestimmen

a) Auf dem Bild siehst du den Graphen einer Ableitungsfunktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h'(x)} . Welche Aussagen kannst du über das Monotonieverhalten von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} machen?

Erinnere dich daran, wie du bei der Berechnung des Monotonieverhaltens vorgehst. Welche Aussagen zum Monotonieverhalten liefert dir Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h'(x)=0} ?

Die Nullstellen von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h'(x)} definieren die verschiedenen Intervalle, in denen das Monotonieverhalten von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h} verschieden ist. Nun kannst du betrachten, auf welchen Intervallen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h'(x)} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <0} bzw. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle >0} ist. Welche Aussagen kannst du damit über das Monotonieverhalten von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} machen?

Die Nullstellen von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h'(x)} sind Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_1=-3, x_2=-2} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_3=-1} .

Damit sind die zu betrachtenden Intervalle Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle ]-\infty, -3[} , Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle ]-3, -2[} , Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle ]-2, -1[} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle ]-1, +\infty[} . Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h'(x)} an diesen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle <0} oder Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle >0} ist.

Für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle ]-\infty, -3[} ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h'(x)<0} , somit ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} auf diesem Intervall streng monoton fallend.

Für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle ]-3, -2[} ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h'(x)>0} , somit ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} auf diesem Intervall streng monoton steigend.

Für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle ]-2, -1[} ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h'(x)<0} , somit ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} auf diesem Intervall streng monoton fallend.

Für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle ]-1, +\infty[} ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h'(x)>0} , somit ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} auf diesem Intervall streng monoton steigend.

b) Zeichne nun mithilfe deiner Ergebnisse aus a) den Funktionsgraphen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} mithilfe deiner Kenntnisse über sein Monotonieverhalten in dein Heft.

Dein Graph könnte in etwa so aussehen:

Möglich, weitere Lösungen für die Zeichnung des Graphen sind unter anderem Verschiebungen in Richtung der Ordinate, also nach unten und oben oder auch Streckungen bzw. Stauchungen.

zurück

Extrema