Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Die Steigung in einem Punkt - die Ableitung als Tangentensteigung

Inhaltsübersicht

a) Unterscheidung Tangente, Sekante und Normale - Aufgabe 1
b) Zuordnungsaufgaben bezüglich der Tangentensteigung - Aufgabe 2, 3, 4 und 5*
c) Untersuchung einer Funktion - Aufgabe 6, 7 und 8*

<popup name="Hinweis zu *"> Die Aufgaben mit einem * sind komplexer.

</popup>

Unterscheidung Tangente, Sekante und Normale

Aufgabe 1

Kannst du die Begriffe unterscheiden? Ordne jedem der drei Begriffe den entsprechenden Graphen zu!

<iframe src="https://learningapps.org/watch?v=p1s1zd2av17" style="border:0px;width:100%;height:400px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>

Aufgabe 2

In diesem Applet siehst du den Graphen einer Funktion, in dem einige Punkte mit roten „Stecknadeln“ markiert sind. Wenn du auf die Punkte klickst, werden dir verschiedene Geraden präsentiert. Wähle dort jeweils die Gerade aus, die der Tangente in dem ausgewählten Punkt entspricht.

Hinweis: Tippe auf das Zeichen für den Vollbildmodus (rechts oben im Applet) und bearbeite die Aufgabe dort.

<iframe src="https://learningapps.org/watch?v=p84w33c8a17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>

<popup name="Hilfe"> Überlege zunächst, wie stark sich der Graph an der jeweiligen Stelle bezüglich der Steigung verändert - Wächst oder fällt er? </popup>

Aufgabe 3

Du siehst im Folgenden den Graphen einer Funktion. Bestimme rechnerisch für die x-Werte unter der Abbildung, welche Steigung m die Tangente an diesen Stellen besitzt.

Hinweis: Wenn du nicht weiterkommst, kannst du auf die Glühbirne oben links im Applet tippen und erhältst einen Tipp.

<iframe src="https://learningapps.org/watch?v=pf4ayrb5j17" style="border:0px;width:100%;height:750px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>

Aufgabe 4

Wahr oder Falsch?

<iframe src="https://learningapps.org/watch?v=psc1spdk517" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>

Aufgabe 5

Tom ist sich nicht sicher, ob die Karten zu der untenstehenden Sinusfunktion gehören.
Kannst du ihm helfen?

Mit dem Regler kannst du die x-Werte im Graphen ändern und erhälst die passende Tangente in dem Punkt.

Teil 1)

<iframe scrolling="no" title="Tangentensteigung beim Sinus" src="https://www.geogebra.org/material/iframe/id/qtyjMzaR/width/700/height/500/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="700px" height="500px" style="border:0px;"> </iframe>

<iframe src="https://learningapps.org/watch?v=p1mo3ok0v17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>

Teil 2) Nachdem du nun die Karten richtig einsortiert hast, erkläre Tom, warum die Karten, die nicht zu der obigen Sinusfunktion passen, falsch sind.

<popup name="Lösung Teil 2">

1) Die Steigung ist zwischen 0 und 2 nicht negativ.

2) Die Steigung ist in allen x-Werten gleich.

3) Da diese Sinusfunktion auf der y-Achse um 2 nach oben verschoben wurde, ändert sich die Steigung in allen Punkten.

4) Die Tangente ist in x = 3 konstant.

</popup>

<popup name="Begründung 1)"> Begründung: Nachdem die Funktion den y-Wert 3 erreicht hat, fällt die Funktion. Somit muss die Steigung negativ werden. </popup> <popup name="Begründung 2)"> Begründung: Die Steigung ist nur in linearen Funktionen (g(x) = m*x + b) gleich. </popup> <popup name="Begründung 3)"> Begründung: Durch die Verschiebung einer Funktion auf der y-Achse verändert sich nicht die Steigung,
sondern es entstehen parallele Tangenten im jeweiligen Punkt. </popup> <popup name="Begründung 4)"> Begründung: Tangenten sind nur an den Extrempunkten konstant. </popup>

c) Untersuchung einer Funktion

Aufgabe 6

Steigung und Koordinaten ablesen

<iframe src="https://learningapps.org/watch?v=piymfh66317" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>

Aufgabe 7

Raupenfahrt

Ein Raupenfahreug mit einer Steigfähigkeit von 76% fährt einen Hang hinauf.
Die Kurve des Hangs lässt sich mit der Funktion f(x)=1/50x² beschreiben.
Für die Bauarbeiten muss die Raupe bis zur Markierungsstange bei x=20 Meter gelangen, schafft sie das?

<iframe src="https://learningapps.org/watch?v=pab2g1ytv17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> <popup name="Lösung"> Legt man ein Steigungsdreieck an die Tangente am Punkt f(20), so kann man beispielweise die Werte f(15)=4 und f(25)=12 ablesen. Die Steigung in % lässt sich durch Δy/Δx*100 bestimmen, nimmt man f(15)=4 und f(25)=12 ist Δx=10 und Δy=8. Die Steigung des Hangs beträgt 80% somit übersteigt diese die Steigfähigkeit der Raupe. </popup>

Aufgabe 8*

Kann es in einem Punkt einer Funktion zwei oder mehr Tangenten geben?!
Luis und Marie sind sich uneinig. Beide schauen sich den untenstehenden Graphen an.
Luis sagt: "Wenn ich mir die Steigung im Punkt P(6/6)anschauen, sehe ich zwei Tangenten."

Marie entgegnet: "Also ich sehe da überhaupt keine Tangente. Da kann gar keine sein, oder?!"

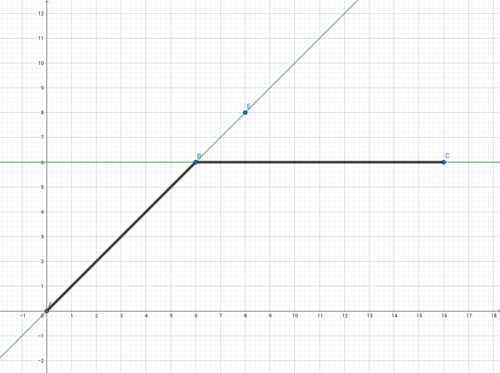
a) Überleg dir, welche zwei Tangenten Luis meint und warum?
Denkst du es gibt hier eine Tangente oder sogar mehrere?
Zeichne Luis` Tangenten mit dem Graphen in dein Heft und ergänze ggf. deine Tangente(n).

<iframe scrolling="no" title="Eine Tangente?" src="https://www.geogebra.org/material/iframe/id/SM67Ex9h/width/700/height/505/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="700px" height="505px" style="border:0px;"> </iframe>

<popup name="Hinweis zu a)">

Hast du dir wirklich Gedanken gemacht?

<popup name="Hinweis a)"> Luis betrachtet die Steigung im Punkt P(6|6).
Dabei schaut er sich die Steigung links und rechts von P an.

</popup>

<popup name="Lösung a)">

Luis hat sich überlegt, wie die Steigung links und rechts vom Punkt P(6|6) ist. Falls es jedoch eine Steigung in einem Punkt einer Funktion gibt, so muss diese eindeutig sein.
Ansonsten ist die Funktion nicht differenzierbar.

</popup>

b) Zeichne die Steigung der Funktion in dein Heft. Du kannst dich auf die Intervalle [0;6] und [6;12] beschränken. Wie verläuft die Steigung und was passiert im Punkt P(6|6)?

<popup name="Lösung b)"> Die Steigung verläuft im Intervall [0;6] und [6;12] linear. Jedoch gibt es im Punkt P(6|6) einen Sprung.
Hier ist die Ableitung also nicht stetig (zusammenhängend) und daher im Intervall [0;12] nicht differenzierbar, wie oben schon zu sehen war.
Damit du die Ableitung in einem Punkt berechnen kannst, muss die Funktion dort auch differenzierbar sein.

<iframe scrolling="no" title="Tangente(n) Punkt P(6|6)?" src="https://www.geogebra.org/material/iframe/id/UbVMmQJr/width/700/height/505/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="800px" height="505px" style="border:0px;"> </iframe>

</popup>