Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung |
(Überschriften) Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 6: | Zeile 6: | ||
* Mit Aufgaben, die <span style="color: #F19E4F"> '''orange''' </span> gefärbt sind, kannst du <span style="color:#F19E4F">'''grundlegende Kompetenzen'''</span> wiederholen und vertiefen. | * Mit Aufgaben, die <span style="color: #F19E4F"> '''orange''' </span> gefärbt sind, kannst du <span style="color:#F19E4F">'''grundlegende Kompetenzen'''</span> wiederholen und vertiefen. | ||
* Aufgaben in <span style="color: #5E43A5"> '''blauer''' </span> Farbe sind Aufgaben <span style="color: #5E43A5">'''mittlerer Schwierigkeit'''</span> | * Aufgaben in <span style="color: #5E43A5"> '''blauer''' </span> Farbe sind Aufgaben <span style="color: #5E43A5">'''mittlerer Schwierigkeit'''</span> und | ||
* | * Aufgaben mit <span style="color: #89C64A"> '''grünem''' </span> Streifen sind <span style="color: #89C64A">'''Knobelaufgaben'''</span>. | ||
Wir wünschen dir viel Erfolg! | Wir wünschen dir viel Erfolg! | ||
| Zeile 16: | Zeile 16: | ||
==Einführung== | ==Einführung== | ||
===Parameterdarstellung einer Geraden=== | Du kannst bereits mit Punkten und Vektoren im Raum umgehen oder hast dieses Thema schon wiederholt. Nun geht es darum, Geraden im Raum zu beschreiben. | ||
===Geraden und ihre Darstellungsformen=== | |||
====Beschreibung einer Geraden im Raum durch Vektoren==== | |||
====Parameterdarstellung einer Geraden==== | |||
{{#ev:youtube|cCetvDxbTQk}} | {{#ev:youtube|cCetvDxbTQk}} | ||
{{Box | 1=Aufgabe 1 | 2=Stelle eine Gleichung einer Geraden in Parameterdarstellung auf, die durch folgende Punkte verläuft: A(1/2/3), B(1/3/4) | 3=Aufgabe}} | {{Box | 1=Aufgabe 1 | 2=Stelle eine Gleichung einer Geraden in Parameterdarstellung auf, die durch folgende Punkte verläuft: A(1/2/3), B(1/3/4) | 3=Aufgabe}} | ||
====Punktprobe==== | |||
===Lagebeziehungen von | ====Spurpunkte einer Geraden==== | ||
====Strecken==== | |||
====Graphische Darstellung von Geraden im Raum==== | |||
===Lagebeziehungen von Gerade=== | |||
{{Box |1= Hinweis |2= In diesem Abschnitt beschäftigst du dich mit der Lagebeziehung von Geraden im Raum. | {{Box |1= Hinweis |2= In diesem Abschnitt beschäftigst du dich mit der Lagebeziehung von Geraden im Raum. | ||
| Zeile 204: | Zeile 217: | ||
|Farbe={{Farbe|grün}}|3= Hervorhebung1}} | |Farbe={{Farbe|grün}}|3= Hervorhebung1}} | ||
====Geraden und ihre Anwendungen==== | |||
Version vom 25. April 2021, 11:56 Uhr
Einführung
Du kannst bereits mit Punkten und Vektoren im Raum umgehen oder hast dieses Thema schon wiederholt. Nun geht es darum, Geraden im Raum zu beschreiben.
Geraden und ihre Darstellungsformen
Beschreibung einer Geraden im Raum durch Vektoren
Parameterdarstellung einer Geraden
Punktprobe
Spurpunkte einer Geraden
Strecken
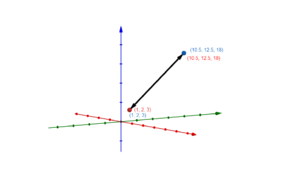
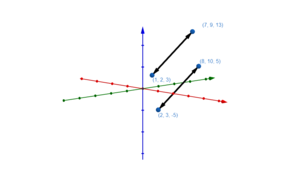
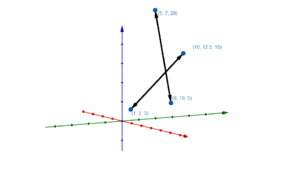
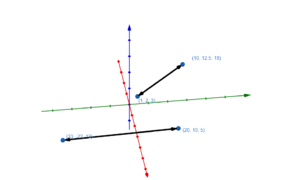
Graphische Darstellung von Geraden im Raum
Lagebeziehungen von Gerade





















![{\displaystyle L={\sqrt[{2}]{x{2}+y^{2}+z^{2}}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/16b4cd0a6bcb59744a3d1428b693be50eb37a42e)







![{\displaystyle 175,49={\sqrt[{2}]{120,2^{2}+96,4^{2}+z^{2}}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/bf27d365fdfc05ec609d2a174adbcee964b6b6d7)


![{\displaystyle L={\sqrt[{2}]{100{2}+80^{2}+70^{2}}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/447380a450e4a2e1e363d5da399f37219f9ea2f1)








