Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 159: | Zeile 159: | ||
{{Box | Aufgabe <Nummer>: <Name> | Inhalt | Arbeitsmethode}} | {{Box | Aufgabe <Nummer>: <Name> | Inhalt | Arbeitsmethode}} | ||
{{Box | Aufgabe <Nummer>: Gerade gesucht | | <nowiki>{{Box | Aufgabe <Nummer>: Gerade gesucht |</nowiki> | ||
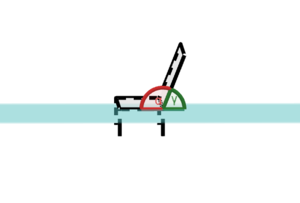
Eine Gerade <math>g</math> soll die <math>x_1-x_2-Ebene </math> in einem Winkel von <math>45 ^\circ</math> schneiden. Über die Gerade <math>g</math> ist nur bekannt, dass sie im Punkt <math>P (1|2|3) </math> beginnt und sie in Richtung des Vektors <math>\vec{x}=\begin{pmatrix} 3\\ 6\\ z \end{pmatrix}</math> verläuft. Stelle die Gerade <math>g</math> auf. | Eine Gerade <math>g</math> soll die <math>x_1-x_2-Ebene </math> in einem Winkel von <math>45 ^\circ</math> schneiden. Über die Gerade <math>g</math> ist nur bekannt, dass sie im Punkt <math>P (1|2|3) </math> beginnt und sie in Richtung des Vektors <math>\vec{x}=\begin{pmatrix} 3\\ 6\\ z \end{pmatrix}</math> verläuft. Stelle die Gerade <math>g</math> auf. | ||
| Zeile 167: | Zeile 167: | ||
{{Lösung versteckt|1=Inhalt|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | {{Lösung versteckt|1=Inhalt|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= Arbeitsmethode}} | ||
==Lagebeziehung Ebene-Ebene== | |||
===Basiswissen=== | |||
{{Box|Aufgabe: Lückentext zur Lagebeziehung zwischen Ebene und Ebene| | |||
== | {{LearningApp|width=100%|height=500px|app=ptpaywm2521}} | ||
|Arbeitsmethode}} | |||
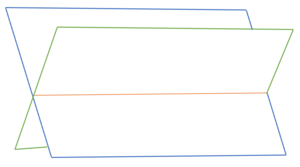
[[Datei:Schnittgerade von zwei Ebenen.png|ohne|rahmenlos]] | [[Datei:Schnittgerade von zwei Ebenen.png|ohne|rahmenlos]] | ||
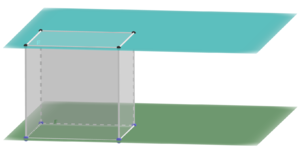
[[Datei:Parallele Ebenen.png|ohne|rahmenlos]] | [[Datei:Parallele Ebenen.png|ohne|rahmenlos]] | ||
{{Box|Untersuchung der Lagebeziehung zwischen zwei Ebenen| | {{Box|Untersuchung der Lagebeziehung zwischen zwei Ebenen| | ||
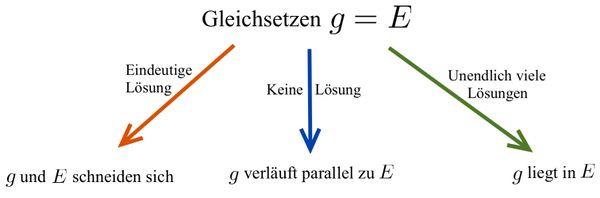
Seien E und F zwei Ebenen im Raum. Um die Lagebeziehung dieser Ebenen zu untersuchen, müssen eine Reihe bestimmter Rechenschritte durchgeführt werden: | Seien E und F zwei Ebenen im Raum. Um die Lagebeziehung dieser Ebenen zu untersuchen, müssen eine Reihe bestimmter Rechenschritte durchgeführt werden: | ||
Schritt 1: Die beiden Ebenengleichungen gleichsetzen | Schritt 1: Die beiden Ebenengleichungen gleichsetzen | ||
Schritt 2: LGS interpretieren | Schritt 2: LGS interpretieren | ||
Schritt 3: Schnittgerade bestimmen | Schritt 3: Schnittgerade bestimmen | ||
| Hervorhebung1}} | | Hervorhebung1}} | ||
{{Box|Aufgabe: Ergebnisse interpretieren| | {{Box|Aufgabe: Ergebnisse interpretieren| | ||
Interpretiere die jeweilige Situation geometrisch. | Interpretiere die jeweilige Situation geometrisch. | ||
c) | a) <math>\begin{vmatrix} 1 & 0 & 0 & -0,5 & 0,5 \\ 0 & 1 & 0 & -1 & 0,5 \\ 0 & 0 & 1 & 1,5 & 1 \end{vmatrix}</math> | ||
b) <math>\begin{vmatrix} 1 & 0 & -1 & -2 & 0 \\ 0 & 1 & -1 & -3 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{vmatrix}</math> | |||
c) <math>\begin{vmatrix} 1 & 0 & -1 & -2 & 1 \\ 0 & 1 & -1 & -3 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{vmatrix}</math> | |||
|Arbeitsmethode}} | |||
{{Box|Aufgabe: Lagebeziehungen berechnen| | |||
Untersuche die Lagebeziehung der jeweiligen Ebenen. | |||
a) <math>E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} </math> | |||
b) <math>E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} </math> | |||
c) <math>E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} </math> | |||
|Arbeitsmethode}} | |||
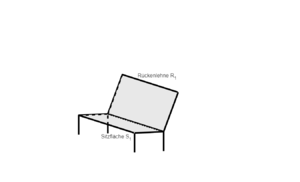
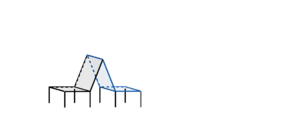
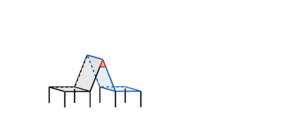
{{Box|Aufgabe: Schnitt von zwei Zeltflächen| | |||
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E: \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}, r,s \in \mathbb{R} </math> und <math>E: \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ -3 \\ 4 \end{pmatrix}, t,u \in \mathbb{R} </math>. Berechne die Geradengleichung der oberen Zeltkante. | |||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
<br /> | |||
{{Box|Aufgabe: Lagebeziehungen berechnen| | {{Box|Aufgabe: Lagebeziehungen berechnen| | ||
Untersuche die Lagebeziehung der jeweiligen Ebenen. | Untersuche die Lagebeziehung der jeweiligen Ebenen. | ||
Version vom 6. Mai 2021, 22:00 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
{{Box | Aufgabe <Nummer>: Gerade gesucht |
Eine Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} soll die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_1-x_2-Ebene } in einem Winkel von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 45 ^\circ} schneiden. Über die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} ist nur bekannt, dass sie im Punkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle P (1|2|3) } beginnt und sie in Richtung des Vektors Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \vec{x}=\begin{pmatrix} 3\\ 6\\ z \end{pmatrix}} verläuft. Stelle die Gerade Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} auf.
Lagebeziehung Ebene-Ebene
Basiswissen
⭐Berechnung des Winkels zwischen Ebene und Ebene