Benutzer:Buss-Haskert/Exponentialfunktion/exponentielles Wachstum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
(Aufgaben ergänzt) Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 30: | Zeile 30: | ||
{{LearningApp|app=17256599|width=100%|heigth=600px}} | {{LearningApp|app=17256599|width=100%|heigth=600px}} | ||
{{Box|Anwendungsaufgabe 1: | {{Box|Anwendungsaufgabe 1: Bevölkerungswachstum|Die Bevölkerung in Indien beträgt zur Zeit 1,38 Milliarden Einwohner (2020). Die jährliche Zunahme beträgt derzeit 0,8%. <br> | ||
Wie viele Einwohner hat Indien im Jahr 2025?|Üben}} | |||
<br> | |||
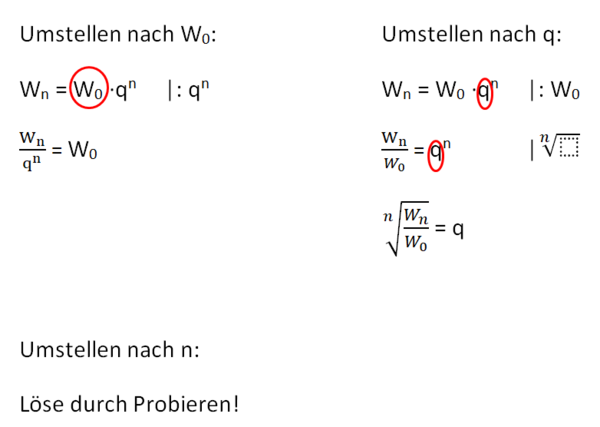
{{Box|Exponentialgleichung - Formel umstellen|[[Datei:Umstellen der Exponentialgleichung.png|rahmenlos|600x600px]]|Arbeitsmethode}} | {{Box|Exponentialgleichung - Formel umstellen|[[Datei:Umstellen der Exponentialgleichung.png|rahmenlos|600x600px]]|Arbeitsmethode}} | ||
{{Box|Anwendungsaufgabe | {{Box|Anwendungsaufgabe 2: Klimawandel|Im Jahr 2021 ist die Fläche der Arktis mit 4,7 Mio km² deutlich kleiner als noch vor rund 30 Jahren. Die Abnahme beträgt mit leichten Schwankungen jährlich ca. 1,7%.<br> | ||
Wie groß war die Fläche vor 30 Jahren?|Üben}} | |||
{{Box|Anwendungsaufgabe 3: Mietpreissteigerung|Die Miete für eine Wohnung stieg innerhalb von 5 Jahren von 600€ auf 730€.<br> | |||
Um wie viel Prozent ist die Miete durchschnittlich pro Jahr gestiegen? |Üben}} | |||
{{Box|Anwendungsaufgabe 4|...(Anwendung n gesucht)|Üben}} | {{Box|Anwendungsaufgabe 4|...(Anwendung n gesucht)|Üben}} | ||
Version vom 27. Dezember 2021, 10:50 Uhr
SEITE IM AUFBAU
Vorwissen
1) Lineares und exponentielles Wachstum (Einstieg)
2) Wachstumsrate und Wachstumsfaktor
3) Exponentielles Wachstum
1) Lineares und exponentielles Wachstum (Einstieg)
2) Wachstumsrate und Wachstumsfaktor
3) Exponentielles Wachstum
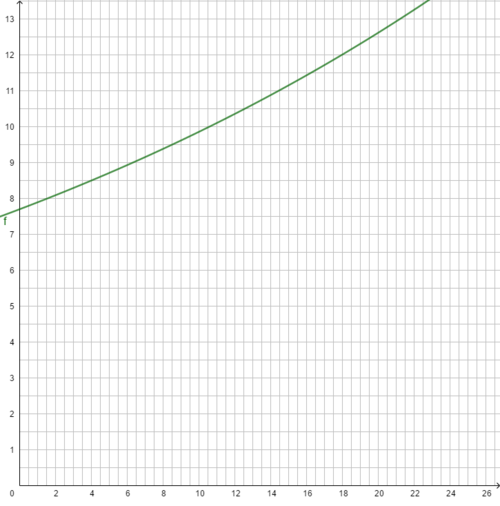
3 Exponentielles Wachstum
Prognose für das Jahr 2030: n = 11
W11 = W0 ∙ q11
= 7,70 ∙ 1,02511
Die Gleichung Wn = W0 · qn heißt Exponentialgleichung, da die Variable n im Exponenten steht.
ÜBUNGSAUFGABEN ERGÄNZEN
- Formel umstellen
- Verdopplungszeit (Bakterien)

Applet von Hegius, R. Schürz
- Halbwertszeit (Atome)

Applet von Hegius, R. Schürz
4 Die Exponentialfunktion

Applet von Ralf Wagner
Der Graph verläuft immer oberhalb der x-Achse.
Der Graph geht immer durch den Punkt (0|1).
Für a>1 steigt der Graph (Zunahme),