Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden verknüpfen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 93: | Zeile 93: | ||
'''c)''' Ebenfalls kam die Frage auf, wie viele Quadratmeter Glasfläche die Reinigungsfirma von außen putzen muss. Beantworte die Frage durch mathematische Rechnungen. | '''c)''' Ebenfalls kam die Frage auf, wie viele Quadratmeter Glasfläche die Reinigungsfirma von außen putzen muss. Beantworte die Frage durch mathematische Rechnungen. | ||
{{Lösung versteckt|1=Die Größe der Glasfläche entspricht der Mantelfläche der Pyramide.|2=Tipp 1 zu c) anzeigen|3=Tipp 1 zu c) verbergen}} | {{Lösung versteckt|1=Die Größe der Glasfläche entspricht der Mantelfläche der Pyramide.|2=Tipp 1 zu c) anzeigen|3=Tipp 1 zu c) verbergen}} | ||
{{Lösung versteckt|1=Du kannst die berechnete Länge eines Stahlträgers aus b) verwenden und damit in einem geeigneten Hilfsdreieck die Seitenhöhe der Pyramide bestimmen.|2=Tipp 2 zu c) anzeigen|3=2 | {{Lösung versteckt|1=Du kannst die berechnete Länge eines Stahlträgers aus b) verwenden und damit in einem geeigneten Hilfsdreieck die Seitenhöhe der Pyramide bestimmen.|2=Tipp 2 zu c) anzeigen|3=Tipp 2 zu c) verbergen}} | ||
{{Lösung versteckt|1=Eine Glaswand besitzt eine Fläche von etwa <math>27,34~\mathrm{m}^2 </math>. Die gesamte Glasfläche der Pyramide beträgt demnach rund <math> 109,34~\mathrm{m}^2 </math>. |2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=Eine Glaswand besitzt eine Fläche von etwa <math>27,34~\mathrm{m}^2 </math>. Die gesamte Glasfläche der Pyramide beträgt demnach rund <math> 109,34~\mathrm{m}^2 </math>. |2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Zeile 129: | Zeile 129: | ||
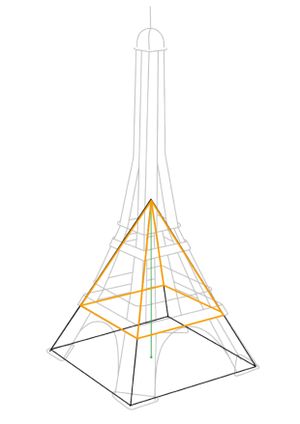
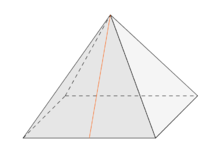
{{Lösung versteckt|1= Du benötigst eine zweite Hilfspyramide zur Berechnung. Diese ist in der folgenden Abbildung orange gekennzeichnet. | {{Lösung versteckt|1= Du benötigst eine zweite Hilfspyramide zur Berechnung. Diese ist in der folgenden Abbildung orange gekennzeichnet. | ||
[[Datei:Skizze Eiffelturm 2.jpg| zentriert | rahmenlos | thumb]] | [[Datei:Skizze Eiffelturm 2.jpg| zentriert | rahmenlos | thumb]] | ||
|2=1 | |2=Tipp 1 zu anzeigen |3=1. Tipp verbergen}} | ||
{{Lösung versteckt|1= Die Stützen haben eine Länge von <math>44,85</math>cm. |2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1= Die Stützen haben eine Länge von <math>44,85</math>cm. |2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Zeile 147: | Zeile 147: | ||
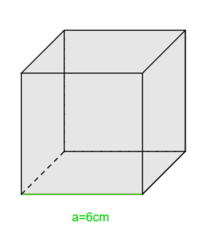
<big>'''a)'''</big> Beschreibe wie sich der Würfel aus den Pyramiden zusammensetzen lässt, wie viele du benötigst, um den Würfel auszufüllen und wie diese Pyramiden aussehen. | <big>'''a)'''</big> Beschreibe wie sich der Würfel aus den Pyramiden zusammensetzen lässt, wie viele du benötigst, um den Würfel auszufüllen und wie diese Pyramiden aussehen. | ||
{{Lösung versteckt|1= Überlege dir eine naheliegende Form für die Grundfläche der Pyramide. |2=1 | {{Lösung versteckt|1= Überlege dir eine naheliegende Form für die Grundfläche der Pyramide. |2=Tipp 1 zu a) anzeigen|3=Tipp 1 a) verbergen}} | ||
{{Lösung versteckt|1= Die Seitenfläche des Würfels entspricht der quadratischen Grundfläche der Pyramide. |2=2 | {{Lösung versteckt|1= Die Seitenfläche des Würfels entspricht der quadratischen Grundfläche der Pyramide. |2=Tipp 2 zu a) anzeigen|3=Tipp 2 zu a) verbergen}} | ||
{{Lösung versteckt|1= Schau dir das Applet an und setze Haken an den verschieden nummerierten Pyramiden, indem du in die leeren Kästchen klickst. Du siehst nun wie die jeweilige Pyramide in dem Würfel liegt und wie alle Pyramiden ihn zusammen ausfüllen. | {{Lösung versteckt|1= Schau dir das Applet an und setze Haken an den verschieden nummerierten Pyramiden, indem du in die leeren Kästchen klickst. Du siehst nun wie die jeweilige Pyramide in dem Würfel liegt und wie alle Pyramiden ihn zusammen ausfüllen. | ||
| Zeile 157: | Zeile 157: | ||
<div style="width:calc(100% - 1rem); height:0; padding-bottom:50%;"><ggb_applet | <div style="width:calc(100% - 1rem); height:0; padding-bottom:50%;"><ggb_applet | ||
id="utuufrpf" width="664" height="332"/></div>|2=3 | id="utuufrpf" width="664" height="332"/></div>|2=Tipp 3 zu a) anzeigen|3= Tipp 3 zu a) verbergen}} | ||
Version vom 14. November 2022, 14:49 Uhr
Checkliste - Das brauchst du
Falls du den Satz des Pythagoras noch einmal wiederholen möchtest, kannst du dein Wissen in Aufgabe 1 auffrischen. Wenn du dich schon sicher im Umgang mit dem Satz des Pythagoras fühlst, kannst du direkt mit Aufgabe 2 fortfahren.
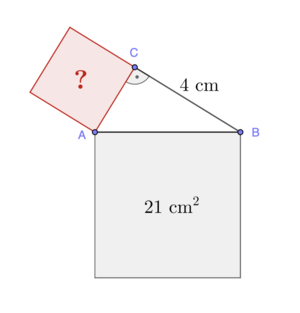
Satz des Pythagoras