Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren/Quadratische Funktionen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 31: | Zeile 31: | ||
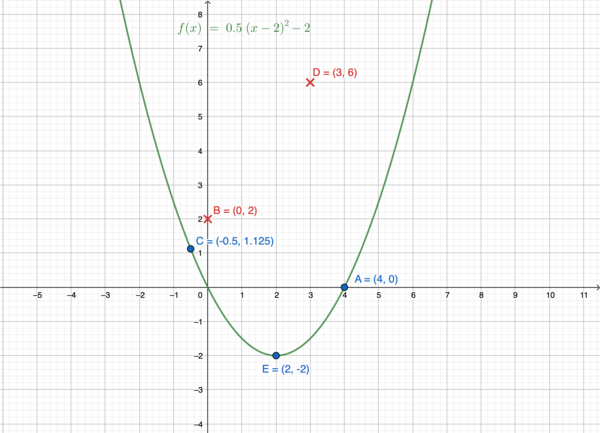
<math>E=(2,-2)</math><br /><br /> | <math>E=(2,-2)</math><br /><br /> | ||
{{LearningApp|width:100%|height:300px|app=ptbc7v3wt19}} | {{LearningApp|width:100%|height:300px|app=ptbc7v3wt19}} | ||
| Zeile 40: | Zeile 39: | ||
{{Box| 3. Welcher Graph hat mit welcher Funktionsgleichung ein Match?|(Zuordnung Funktionsgraph und Funktionsgleichung.) | {{Box| 3. Welcher Graph hat mit welcher Funktionsgleichung ein Match?|(Zuordnung Funktionsgraph und Funktionsgleichung.) | ||
|Arbeitsmethode}} | |||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
| Zeile 46: | Zeile 45: | ||
{{Box| 4. Aus dem Graphen eine quadratische Funktion in Scheitelpunktsform aufstellen| | {{Box| 4. Aus dem Graphen eine quadratische Funktion in Scheitelpunktsform aufstellen| | ||
{{LearningApp|width:100%|height:300px|app=pke0t2avt19}} | {{LearningApp|width:100%|height:300px|app=pke0t2avt19}} | ||
Version vom 24. April 2019, 12:23 Uhr
Scheitelpunktform
Wir schauen uns die Funktion an. Funktionen dieser Art heißen qua dra tisch e Funktionen. Der Graph einer solchen Funktion ist eine Pa ra bel. Der höchste bzw. der tiefste Punkt eines solchen Funktionsgraphen heißt Schei tel punkt.
Ist der Parameter a kleiner als Null (a<0), dann ist der Graph der Funktion g nach un ten geöffnet.
Ist a größer als Null (<>0), dann ist der Graph von g nach o ben geöffnet.
Ist a größer als Eins (a>1) oder kleiner als minus Eins (a<-1), dann wird der Graph von g schma ler. Man sagt, dass in diesem Fall der Graph ge streckt wird.
Ist d größer als Null (d>0), dann wird der Graph von g nach rechts verschoben.
Ist d kleiner als Null (d<0), dann wird der Graph von g nach links verschoben.
Ist e kleiner als Null (e<0), dann wird der Graph von g nach un ten verschoben.
Ist e größer als Null (e>0), dann wird der Graph von g nach o ben verschoben.
Umwandlung Scheitelpunktform und Normalenform














































![{\displaystyle {\begin{array}{rlll}j(x)&=&-0.0075\cdot x^{2}+1.2\cdot x+1&\mid -0.0075\,ausklammern\\&=&-0.0075(x^{2}-160x-{\frac {400}{3}})&\mid +80^{2}-80^{2}\,quadratische\,Erg{\ddot {a}}nzung\\&=&-0.0075(x^{2}-160x+80^{2}-80^{2}-{\frac {400}{3}})&\mid 2.\,binomische\,Formel\\&=&-0.0075[(x-80)^{2}-{\frac {19600}{3}}]&\mid ausmultiplizieren\\&=&-0.0075(x-80)^{2}+49\end{array}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/db0be9404b12821f37c38e64bd0fb7f9875c16d6)
















