Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Wendepunkte

Merke: Definition

Ein Wendepunkt beschreibt einen Punkt auf einem Funktionsgraphen an dem sich das Krümmungsverhalten des Graphes ändert. Der Funktionsgraph ändert an dieser Stelle seine Krümmung von rechts nach links (Rechts-links-Wendestelle, kurz: RLW) oder von links nach rechts (Links-rechts-Wendestelle, kurz: LRW).

Tipp: Es kann helfen, wenn man sich vorstellt auf dem Graphen mit einem Fahrrad zu fahren, so ist der Wendepunkt genau an dem Punkt, wo sich die Richtung, in die man lenkt, ändert.

Aufgabe 1 - Wendepunkte angeben

Gib die Wendepunkte im Graphen an.

Merke: Definition 2

An einem Wendepunkt $x_{W}$ einer Funktion $f(x)$ ist die Steigung in der näheren Umgebung maximal bzw. minimal. Somit folgt, dass die Ableitung an dieser Stelle ein lokales Extremum aufweist. Daraus ergibt sich das notwendige Kriterium für einen Wendepunkt. Aus dem vorherigen Kapitel haben wir gelernt: Wenn die Funktion $f'(x)$ im Punkt $x_{W}$ einen Extrempunkt aufweist, so ist die Ableitung dieser Funktion $f''(x)$ in diesem Punkt gleich 0. Das hinreichende Kriterium ergibt sich, wie im vorherigen Kapitel.

Zusammenfassung:

• notwendiges Kriterium: $f''(x_{W})=0$
• hinreichendes Kriterium: $f'''(x_{W})\neq 0$, Wobei gilt: $f'''(x_{W})>0\Rightarrow$RLW oder $f'''(x_{W})<0\Rightarrow$LRW

Berechnen des Wendepunktes

• Notwendiges Kriterium: Nullstellen $x_{W}$ der zweiten Ableitung berechnen

• Hinreichendes Kriterium: Einsetzen der berechneten Funktionstherms $x_{W}$ in die dritte Ableitung (RLW oder LRW?)

• Berechnen des Funktionswertes durch einsetzen des Funktionstherms $x_{W}$ in die Ursprüngliche Funktion

Du kannst dir noch gerne das folgende Beispiel anschauen:

Beispiel: Gegeben sei die Funktion $f(x)={\frac {7}{12}}x^{4}-5x^{2}-90.000$

• Notwendiges Kriterium: $f''(x_{W})=0$

$f'(x)={\frac {28}{12}}x^{3}-10x$

$f''(x)={\frac {84}{12}}x^{2}-10=7x^{2}-10$

$f'''(x)=14x$

$f''(x_{W})=7x_{W}^{2}-10=0$

$\Rightarrow x_{W}^{2}={\frac {10}{7}}$

$\Rightarrow x_{W}=\pm {\sqrt {\frac {10}{7}}}$

$\Rightarrow x_{W_{1}}=+{\sqrt {\frac {10}{7}}}$ und $x_{W2}=-{\sqrt {\frac {10}{7}}}$

• Hinreichendes Kriterium: $f'''(x_{W})\neq 0$

$f'''(x_{W_{1}})=20>0$ und $f'''(x_{W_{2}})=-20<0$

$\Rightarrow$An $x_{W_{1}}$ liegt eine Recht-links-Wendestelle und an $x_{W_{2}}$ eine Links-rechts-Wendestelle vor.

• Berechnen der Funktionswerte:

$f(x_{W_{1}})={\frac {7}{12}}\cdot 20^{4}-5\cdot 20^{2}-90.000={\frac {4.000}{3}}\approx 1.333,33$ $f(x_{W_{2}})={\frac {7}{12}}\cdot (-20)^{4}-5\cdot (-20)^{2}-90.000={\frac {4.000}{3}}\approx 1.333,33$

Lösung: An dem Punkt $(20/{\frac {4.000}{3}})$ liegt eine Recht-links-Wendepunkt vor und an dem Punkt $(-20/{\frac {4.000}{3}})$ liegt ein Links-rechts-Wendepunkt vor.

Und nun du...

Aufgabe 2 - Wendepunkt bestimmen

Berechne die Wendepunkte der folgenden Funktionen. Falls du Hilfe brauchst, schaue dir zunächst die Tipps an. Beachte: Der Aufgabenteil b) geht über Funktionsscharen und ist nur für den LK gedacht.

a)$g(x)={\frac {2}{25}}x^{5}-x^{3}+{\frac {25}{8}}x$

Schaue dir das obige Beispiel nochmal genau an!

Versuche die drei Ableitungen von der Funktion zu berechnen und schaue dir dann die Kriterien für einen Wendepunkt an!

Um die Nullstelle eine Polynoms dritten Grades zu berechnen, musst du ein $x$ ausklammern.

Schaue dir hier die Rechnung an um den Lösungsweg schrittweise nachzuvollziehen!

• Notwendiges Kriterium: $g''(x_{W})=0$

$g'(x)={\frac {10}{25}}x^{4}-3x^{2}+{\frac {25}{8}}$

$g''(x)={\frac {40}{25}}x^{3}-6x={\frac {8}{5}}x^{3}-6x$

$g'''(x)={\frac {24}{5}}x^{2}-6$

$g''(x_{W})={\frac {8}{5}}x_{W}^{3}-6x_{W}=0$ Polynom dritten Grades: $x_{W}$ ausklammern.

$\Rightarrow x_{W}\cdot ({\frac {8}{5}}x_{W}^{2}-6)=0$ Wir erhalten drei Lösungen ...

$\Rightarrow x_{W_{1}}=0$ und $({\frac {8}{5}}x_{W_{2/3}}^{2}-6)=0$ Die Gleichung muss in die Form $x^{2}+px+q$ gebracht werden, um die pq-Formel anzuwenden.

$\Rightarrow (x_{W_{2/3}}^{2}-6\cdot {\frac {5}{8}})=0$, also $\Rightarrow p=0,q=-{\frac {30}{8}}$

$\Rightarrow x_{W_{2/3}}=-{\frac {0}{2}}\pm {\sqrt {({\frac {0}{2}})^{2}+{\frac {30}{8}}}}$

$\Rightarrow x_{W_{2/3}}=\pm {\sqrt {\frac {30}{8}}}$

$\Rightarrow x_{W_{2}}=+{\sqrt {\frac {30}{8}}}$ und $x_{W_{3}}=-{\sqrt {\frac {30}{8}}}$

• Hinreichendes Kriterium: $f'''(x_{W})\neq 0$

$g'''(x_{W_{1}})={\frac {24}{5}}\cdot 0^{2}-6=-6<0$

$g'''(x_{W_{2}})={\frac {24}{5}}\cdot ({\sqrt {\frac {30}{8}}})^{2}-6=9>0$

$g'''(x_{W_{3}})={\frac {24}{5}}\cdot (-{\sqrt {\frac {30}{8}}})^{2}-6=9>0$

$\Rightarrow$An $x_{W_{1}}$ liegt eine Links-rechts-Wendestelle und an $x_{W_{2}}$ und $x_{W_{3}}$ eine Rechts-links-Wendestelle vor.

• Berechnen der Funktionswerte:

$g(x_{W_{1}})={\frac {2}{25}}\cdot 0^{5}-0^{3}+{\frac {25}{8}}\cdot 0=0$

$g(x_{W_{2}})={\frac {2}{25}}\cdot ({\sqrt {\frac {30}{8}}})^{5}-({\sqrt {\frac {30}{8}}})^{3}+{\frac {25}{8}}\cdot {\sqrt {\frac {30}{8}}}\approx 0,97$ $g(x_{W_{3}})={\frac {2}{25}}\cdot (-{\sqrt {\frac {30}{8}}})^{5}-(-{\sqrt {\frac {30}{8}}})^{3}+{\frac {25}{8}}\cdot {\sqrt {-{\frac {30}{8}}}}\approx -0,97$

Lösung: An dem Punkt $(0/0)$ liegt eine Links-rechts-Wendepunkt vor und an den Punkten $({\sqrt {\frac {30}{8}}}/0,97)$ und $(-{\sqrt {\frac {30}{8}}}/-0,97)$ liegen Rechts-links-Wendepunkte vor.

b) $h(x)=x^{3}-{\frac {a}{2}}x^{2}-a$

Schaue dir das obige Beispiel nochmal genau an!

Versuche die drei Ableitungen von der Funktionsschar zu berechnen und schaue dir dann die Kriterien für einen Wendepunkt an!

Die Variable $a$ kannst du wie eine Zahl behandeln!

Schaue dir hier die Rechnung an um den Lösungsweg schrittweise nachzuvollziehen!

• Notwendiges Kriterium: $h''(x_{W})=0$

$h'(x)=3x^{2}-ax$

$h''(x)=6x-a$

$h'''(x)=6$

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h''(x_{W}) = 6x_W-a =0 }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow x_{W}=\frac{a}{6} } Es existiert ein Wendepunkt.

• Hinreichendes Kriterium: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'''(x_W)\neq 0}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h'''(x_{W}) = 6 > 0}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow} Bei dem Wendepunkt handelt es sich um einen Recht-links-Wendepunkt.

• Berechnen des Funktionswertes:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x_{W}) = (\frac{a}{6})^3-\frac{a}{2}\cdot(\frac{a}{6})^2-a=a^3\cdot(\frac{1}{6^3}-\frac{1}{2\cdot 6^2})-a=a^3\cdot(\frac{1}{6^3}-\frac{3}{3\cdot 2\cdot 6^2})-a=-\frac{2}{6^3}a^3-a}

Lösung: Die Rechts-links-Wendepunkt der Funktionsscharen liegen an den Punkten: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (\frac{a}{6}/-\frac{2}{6^3}a^3-a) } .

Aufgabe 3 - Die schnelle Achterbahn

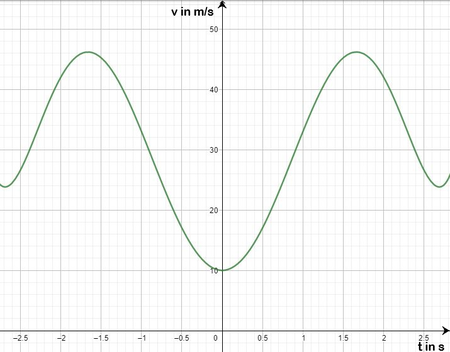
Im Europa Park in Baden-Württemberg soll eine schnelle Achterbahn gebaut werden. Kurz vor Schluss soll die Bahn über zwei hohe Punkte fahren und dort die Höchstgeschwindigkeiten erreichen. Die Mitarbeiter des Parks haben eine Simulation der Achterbahn erstellt und haben somit die Geschwindigkeit der Achterbahn gegen die Zeit aufgenommen. Die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v(t)=\frac{1}{2}t^6-\frac{15}{2}t^4+30t^{2}+10 } (siehe Abbildung) beschreibt im Intervall [-3s,3s] sehr gut die Geschwindigkeit der Achterbahn am Ende der Fahrt.

An den Stellen, wo die Achterbahn stark abbremst oder beschleunigt sind die wichtigsten Stellen der Fahrt. Zu diesen Zeitpunkten sollen deshalb besondere Sicherheitssysteme arbeiten. Gebe mit Hilfe der Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v(t) } an, zu welchen Zeitpunkten die Beschleunigung minimal bzw. maximal ist.

Die Beschleunigung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a(t)} kann man ermittel, da sie der Ableitung der Geschwindigkeit entspricht also: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a(t)=v'(t)} . Die Geschwindigkeit ist angegeben. Was gilt für die Punkte, wo die Beschleunigung maximal oder minimal ist? Lösung zu der Frage findest du in Tipp 2.

Zu dem Zeitpunkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t_{W}} an dem die Beschleunigung maximal bzw. minimal ist gilt: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a'(t_{W})=0} , da zu diesem Zeitpunkt die Beschleunigung eine Extremstelle und somit die Geschwindigkeit einen Wendepunkt aufweist.

Hier muss also nur wieder der Wendepunkt berechnet werden. Falls du noch mehr Hilfe brauchst, schau dir die Tipps von Aufgabe 2 und das Beispiel nochmal an!

Schaue dir hier die Rechnung an um den Lösungsweg schrittweise nachzuvollziehen!

• Notwendiges Kriterium: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v''(t_{W})=a'(t_{W})=0} , wobei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a(t)} die Beschleunigung der BAhn beschreibt.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v(t)=\frac{1}{2}t^6-\frac{15}{2}t^4+30t^{2}+10 }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v'(t)=a(t)=3t^5-30t^3+60t }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v''(t)=a'(t)=15t^4-90t^2+60 }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v'''(t)=a''(t)=60t^3-180t }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0=v''(t_{W})=a'(t_{W})=15t_{W}^4-90t_{W}^2+60} Substitution notwndig: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t_{W}^2= z }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow 0=15z^2-90z+60} Die Gleichung muss in die Form Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x^2+px+q} gebracht werden, um die pq-Formel anzuwenden.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow 0=z^2-6z+4} pq-Formel anwenden mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle p=-6} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle q=4}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow z_{1/2}=\frac{6}{2}\pm \sqrt {(\frac{6}{2})^2-4}}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow z_{1/2}=3\pm \sqrt {5}}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow z_{1}=3 + \sqrt {5}} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow z_{2}=3 - \sqrt {5}} Nun müssen wir zurück substituieren Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle z=t_{W}^2}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow t_{W_{1/2}}=(3 + \sqrt {5})^2} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow t_{W_{3/4}}=(3 - \sqrt {5})^2}

• Hinreichendes Kriterium: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'''(x_W)\neq 0}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'''(x_{W1})=-6} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'''(x_{W2})=} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'''(x_{3})=}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow} an Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_{W1}} liegt eine Recht-links-Wendestelle, an Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {x_W2}} eine Links-rechts-Wendestelle vor und an Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {x_W2}} eine Links-rechts-Wendestelle vor.

Lösung: An dem Punkt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (0/0)} liegt eine Links-rechts-Wendepunkt vor und an den Punkten Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (\sqrt{\frac{30}{8}}/0,97)} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (-\sqrt{\frac{30}{8}}/-0,97)} liegen Rechts-links-Wendepunkte vor.

zurück

Verhalten im Unendlichen und nahe Null