Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der Randfunktion zur Integralfunktion

Infoboxen

Was ist ein Integral?

Die Fläche unter einem Graphen kann durch den gemeinsamen Grenzwert von Ober- und Untersummenfolgen bestimmt werden. Dies nennt man das Integral von $f$ über das Intervall $[a;b]$ und schreibt dafür $\int _{a}^{b}f(x)dx$. 

Die Funktion $f$ heißt dann über $[a;b]$ integrierbar. Dabei ist $a$ die untere und $b$ die obere Integrationsgrenze und $f$ die Integrandfunktion.

Betrachtet man die Werte von Integralen in Abhängigkeit von einer festen unteren Grenze $a$ und einer variablen (anstelle einer festen) oberen Grenze $x$ und verwendet deshalb $t$ als Variable der Integrandfunktion $f$, so erhält man eine Integralfunktion $F_{a}(x)=\int _{a}^{x}f(t)dt,x\in [a;b].$

$F_{a}$ ist also eine Funktion, die jedem $x\in [a;b]$ das Integral von $f$ über $[a;x]$ zuordnet. $x$ ist dabei die Funktionsvariable, in sie darf eingesetzt werden, während $t$ eine gebundene Variable ist, in die nicht eingesetzt werden darf.

Eine Funktion $F$ heißt Stammfunktion zur Funktion $f$, wenn gilt $F'(x)=f(x)$ für alle $x\in (a;b)$.

Partielle Integration

Die partielle Integration ist eine Methode, die die Integration von Produkten zweier Funktionen ermöglicht. Sie beruht auf der Produktregel und wird daher auch Produktintegration genannt. Dabei ist es von Vorteil, wenn die eine Funktion leicht abzuleiten und die andere leicht zu integrieren ist.

Allgemein definiert man die Formel der partiellen Integration so:$\int f'(x)*g(x)\,dx=[f(x)*g(x)]-\int f(x)*g'(x)\,dx$

Dabei ist $\int f'(x)*g(x)\,dx$ das ursprüngliche Integral.

$f'(x)$ ist die leicht zu integrierende Funktion.

$g(x)$ ist die leicht abzuleitende Funktion.

Falls du eine ausführliche Erklärung mit einem Beispiel benötigst,klicke hier.

Beispiel zur partielle Integration

Die Beispielfunktion lautet: $h(x)=e^{x}*x$

$e^{x}$ lässt sich leicht integrieren. Also $f(x)=e^{x}$ und $f'(x)=e^{x}$

$x$ lässt sich leicht ableiten. Also $g(x)=x$ und $g'(x)=1$

Nun müssen unsere Funktionen und deren Ableitungen in die oben genannte Formel eingesetzt werden: $\int f'(x)*g(x)\,dx=[f(x)*g(x)]-\int f(x)*g'(x)\,dx$ $\int e^{x}*x\,dx=[e^{x}*x]-\int e^{x}*1\,dx=[e^{x}*x]-[e^{x}]=e^{x}*(x-1)$

Die integrierte Funktion bzw. Stammfunktion von $h(x)=e^{x}*x$ lautet somit:$H(x)=e^{x}*(x-1)$

Integration durch Substitution

Die Integration durch Substitution ist eine weitere Methode der Integration, welche auf der Kettenregel beruht. Dabei muss eine Verknüpfung zweier Funktionen innerhalb dieses Integrals vorhanden sein. Allgemein wird ihre Formel folgendermaßen definiert:$\int _{a}^{b}f(g(x))*g'(x)\,dx=\int _{g(a)}^{g(b)}f(z)\,dx$

Vorgehen:

1. Zunächst wird die innere Funktion $g(x)$ dieser verknüpften Funktion durch eine Variable z ersetzt. Also $z=g(x)$
2. Die Gleichung wird nach x abgeleitet. Also $z=g(x)\Longrightarrow dz=g'(x)dx$
3. und dann nach dx umgeformt: $dz=g'(x)dx\Longrightarrow dx={\frac {dz}{g'(x)}}$
4. Falls im Integral die Grenzen a und b angegeben wurden, müssen diese durch Einsetzen in die Gleichung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x) } angepasst werden: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a \longrightarrow g(a) } neue untere Grenze Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle b \longrightarrow g(b) } neue obere Grenze
5. Die nach dx umgeformte Gleichung und die neuen Grenzen werden nun in das Integral eingesetzt.
6. Nun folgt das normale Integrationsverfahren.
7. Resubstitution: Zuletzt wird für z wieder die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x) } eingesetzt.

Beispiel für Integration durch Substituion

Die zu integrierende Funktion lautet: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)=e^{2x} }

Zu bestimmen: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle H(x) = \int_a^b e^{2x}\, dx }

1. Die innere Funktion ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x) = 2x = z }
2. Ableitung der Funktion: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g'(x)=2 *dx=dz }
3. Umformen nach dx: $2*dx=dz\Longrightarrow dx={\frac {dz}{2}}$
4. Anpassung der alten Grenzen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a \longrightarrow g(a)} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle b \longrightarrow g(b) }
5. Einsetzen in das Integral: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \int_{g(a)}^{g(b)} e^z\, \frac{dz}{2} = \frac{1}{2} * \int_{g(a)}^{g(b)} e^z\, dz }
6. Integration: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{2} * \int_{g(a)}^{g(b)} e^z\, dz = \frac{1}{2} \left [ e^z\right ]^{g(b)}_{g(a)} }
7. Die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x) } für die Variable Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle z } ersetzen: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{2} \left [ e^z\right ]^{g(b)}_{g(a)} = \frac{1}{2} \left [ e^{2x}\right ]^{g(b)}_{g(a)} }

Die integrierte Funktion bzw. Stammfunktion von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)=e^{2x} } lautet: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle H(x) = \frac{1}{2} * e^{2x} }

Rotationskörper und Raumintegrale

Lässt man den Graphen einer Funktion um die x-Achse rotieren, so entsteht ein sogenannter Rotationskörper. Für seinen Rauminhalt gilt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V_{rot} = \pi \int_{a}^{b} ( f(x) )^2 dx}
. 

Als Beispiel betrachten wird das Volumen einer Kugel mit Radius Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r} , die durch die Rotation des Graphen der Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x) = \sqrt{r^2-x^2}} im Intervall Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle [-r; r]} um die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} -Achse entsteht. Mit der Formel für den Rotationskörper erhält man nun das Volumen der Kugel: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V = \pi\int_{-r}^{r}(r^2-x^2) dx = \left[\pi(r^2\cdot x - \frac{1}{3}x^3)\right]_{-r}^{r} = \frac{4}{3}\pi\cdot r^3}

Aufgaben

Übung 1

Wie lautet die Stammfunktion dieser Funktionen?

a) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x) = x*sin(2x) }

Nutze die partielle Integration

Setze die leicht abzuleitende Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)=x } und die leicht zu integrierende Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f'(x)=sin(2x)}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F(x)= \frac{sin(2x)}{4} - \frac{x*cos(2x)}{2} + C }

b) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)=x*e^{x^2} }

Nutze die Integration durch Substitution

Setze die innerer Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)=x^2 = z } und leite sie nach x ab

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \int x*e^z\, \frac{dz}{2x} = \int \frac{e^z}{2}\, dz = \frac{1}{2} \int e^z\, dz }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F(x)= \frac{e^{x^2}}{2} + C }

c) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)= \frac{e^x}{a-e^x} }

Nutze die Integration durch Substitution

Setze die innerer Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)= a-e^x = z } und leite sie nach x ab

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle F(x)= - ln(|a-e^x|) + C }

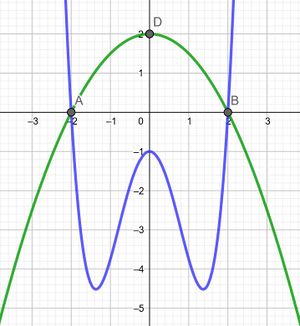
Textaufgabe: Zahn-Logo für eine Praxis

In einer Zahnarztpraxis soll ein neues Logo entworfen werden. Dazu wurde die nebenstehende Zeichnung angefertigt, welche durch die Funktionen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)=- \frac{x^2}{2} + 2 } und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)= x^4- \frac{15}{4} * x^2 - 1 } das Zahnlogo bildet. Dabei entspricht eine Längeneinheit in dem Graphen 1 cm. Nun soll dieses Logo mit einer Dicke von 1 mm aus Silber (Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1 cm^2 } Silber wiegt 10,5 g) produziert werden. Wie schwer wird das Logo dann werden?

Skizze des Zahn-Logos

Zuerst muss die Fläche des Logos berechnet werden. Dazu wird dieses Integral genötigt: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \int_{-2}^2 f(x) + g(x)\, dx }

Hast du daran gedacht, alle Einheiten einheitlich anzupassen? Die Dicke von 1 mm muss auf jeden Fall noch in cm umgerechnet werden.

Wenn du die Fläche des Logos Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A_{Logo} } wie in Tipp 1 berechnet hast, kannst du das Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V_{Logo}} nun durch das Produkt von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A_{Logo} } und der Dicke (beachte Tipp 2!) berechnen

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A_{Logo} = 3,2 cm^2 }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V_{Logo}= A_{Logo} * Dicke_{Logo} = 3,2 {cm}^2 * 0,1 cm = 0,32 {cm}^3 }

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V_{Logo}*Gewicht_{Silber}= 0,32 [{cm}^3] * 10,5 [g] = 3,36 [g] }

Das fertige Logo aus Silber wiegt 3,36 g.

<iframe src="https://learningapps.org/watch?v=pa1tk2o5v20" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>