Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der Randfunktion zur Integralfunktion

Informationen

Einführung: Integral

Was ist ein Integral?

Die Fläche unter einem Graphen kann durch den gemeinsamen Grenzwert von Ober- und Untersummenfolgen bestimmt werden. Dies nennt man das Integral von $f$ über das Intervall $[a;b]$ und schreibt dafür $\int _{a}^{b}f(x)dx$.

Die Funktion $f$ heißt dann über $[a;b]$ integrierbar. Dabei ist $a$ die untere und $b$ die obere Integrationsgrenze und $f$ die Integrandfunktion.

Betrachtet man die Werte von Integralen in Abhängigkeit von einer festen unteren Grenze $a$ und einer variablen (anstelle einer festen) oberen Grenze $x$ und verwendet deshalb $t$ als Variable der Integrandfunktion $f$, so erhält man eine Integralfunktion $F_{a}(x)=\int _{a}^{x}f(t)dt,x\in [a;b].$

$F_{a}$ ist also eine Funktion, die jedem $x\in [a;b]$ das Integral von $f$ über $[a;x]$ zuordnet. $x$ ist dabei die Funktionsvariable, in sie darf eingesetzt werden, während $t$ eine gebundene Variable ist, in die nicht eingesetzt werden darf.

Eine Funktion $F$ heißt Stammfunktion zur Funktion $f$, wenn gilt $F'(x)=f(x)$ für alle $x\in (a;b)$.

Mittelwerte mithilfe des Integrals bestimmen

Der Mittelwert einer Funktion lässt sich über das Integral bestimmen.

Bezeichnen wir mit f eine Funktion. Der Mittelwert einer Funktion f lässt sich auf dem Intervall $[a;b]$ berechnen. Hierzu benötigst du folgende Formel: $M={\frac {1}{b-a}}\int _{a}^{b}f(x)\,dx$

Beispiel:

Ein Auto beschleunigt 40 Sekunden lang. Die Geschwindigkeit zum Zeitpunkt t ist gegeben durch $f(t)={\frac {5}{4}}*t$, wobei t in Sekunden und die Funktion f(t) in m/s angegeben wird. Wie groß ist die Durchschnittsgeschwindigkeit?

Vorgehen zur Bearbeitung der Testaufgabe:

1. Benutzung der Formel

$M={\frac {1}{b-a}}\int _{a}^{b}f(x)\,dx$

1. Einsetzen der Gegebenheiten in die Formel:

$M={\frac {1}{40-0}}\int _{40}^{0}{\frac {5}{4}}*t\,dt$

1. Ausrechnen:

$M={\frac {1}{40-0}}\int _{40}^{0}{\frac {5}{4}}*t\,dt={\frac {1}{30}}*[{\frac {5}{8}}*t^{2}]_{40}^{0}={\frac {1}{40}}*{\frac {1}{40}}*40^{2}=25$

1. Antwortsatz formulieren:

Die Durchschnittsgeschwindigkeit betrug beim Auto 25 m/s.

Rechnen mit Integralen

Übung 1

Welche der folgenden Rechenregeln sind richtig und welche falsch?

Additivität des Integrals:

1 $\int _{a}^{c}f(x)dx=\int _{a}^{b}f(x)dx-\int _{b}^{c}f(x)dx$

	Wahr
	Falsch

2 $\int _{a}^{c}f(x)dx=\int _{a}^{b}f(x)dx+\int _{b}^{c}f(x)dx$

	Wahr
	Falsch

3 $\int _{a}^{c}f(x)dx=\int _{a}^{b}f(x)dx+\int _{a}^{c}f(x)dx$

	Wahr
	Falsch

Regel vom konstanten Faktor:

1 $\int _{a}^{b}c\cdot f(x)dx=c\cdot \int _{a}^{b}f(x)dx$

	Wahr
	Falsch

2 $\int _{a}^{b}c\cdot f(x)dx=c^{2}\cdot \int _{a}^{b}f(x)dx$

	Wahr
	Falsch

3 $\int _{a}^{b}c\cdot f(x)dx=c+\int _{a}^{b}f(x)dx$

	Wahr
	Falsch

Summenregel:

Partielle Integration

Partielle Integration

Die partielle Integration ist eine Methode, die die Integration von Produkten zweier Funktionen ermöglicht. Sie beruht auf der Produktregel und wird daher auch Produktintegration genannt. Dabei ist es von Vorteil, wenn die eine Funktion leicht abzuleiten und die andere leicht zu integrieren ist.

Allgemein definiert man die Formel der partiellen Integration so:$\int f'(x)*g(x)\,dx=[f(x)*g(x)]-\int f(x)*g'(x)\,dx$

Dabei ist $\int f'(x)*g(x)\,dx$ das ursprüngliche Integral.

$f'(x)$ ist die leicht zu integrierende Funktion.

$g(x)$ ist die leicht abzuleitende Funktion.

Falls du eine ausführliche Erklärung mit einem Beispiel benötigst,klicke hier.

Beispiel zur partielle Integration

Die Beispielfunktion lautet: $h(x)=e^{x}*x$

$e^{x}$ lässt sich leicht integrieren. Also $f(x)=e^{x}$ und $f'(x)=e^{x}$

$x$ lässt sich leicht ableiten. Also $g(x)=x$ und $g'(x)=1$

Nun müssen unsere Funktionen und deren Ableitungen in die oben genannte Formel eingesetzt werden: $\int f'(x)*g(x)\,dx=[f(x)*g(x)]-\int f(x)*g'(x)\,dx$ $\int e^{x}*x\,dx=[e^{x}*x]-\int e^{x}*1\,dx=[e^{x}*x]-[e^{x}]=e^{x}*(x-1)$

Die integrierte Funktion bzw. Stammfunktion von $h(x)=e^{x}*x$ lautet somit:$H(x)=e^{x}*(x-1)$

Integration durch Substitution

Integration durch Substitution

Die Integration durch Substitution ist eine weitere Methode der Integration, welche auf der Kettenregel beruht. Dabei muss eine Verknüpfung zweier Funktionen innerhalb dieses Integrals vorhanden sein. Allgemein wird ihre Formel folgendermaßen definiert:$\int _{a}^{b}f(g(x))*g'(x)\,dx=\int _{g(a)}^{g(b)}f(z)\,dx$

Vorgehen:

1. Zunächst wird die innere Funktion $g(x)$ dieser verknüpften Funktion durch eine Variable z ersetzt. Also $z=g(x)$
2. Die Gleichung wird nach x abgeleitet. Also $z=g(x)\Longrightarrow dz=g'(x)dx$
3. und dann nach dx umgeformt: $dz=g'(x)dx\Longrightarrow dx={\frac {dz}{g'(x)}}$
4. Falls im Integral die Grenzen a und b angegeben wurden, müssen diese durch Einsetzen in die Gleichung $g(x)$ angepasst werden: $a\longrightarrow g(a)$ neue untere Grenze $b\longrightarrow g(b)$ neue obere Grenze
5. Die nach dx umgeformte Gleichung und die neuen Grenzen werden nun in das Integral eingesetzt.
6. Nun folgt das normale Integrationsverfahren.
7. Resubstitution: Zuletzt wird für z wieder die Funktion $g(x)$ eingesetzt.

Beispiel für Integration durch Substituion

Die zu integrierende Funktion lautet: $h(x)=e^{2x}$

Zu bestimmen: $H(x)=\int _{a}^{b}e^{2x}\,dx$

1. Die innere Funktion ist $g(x)=2x=z$
2. Ableitung der Funktion: $g'(x)=2*dx=dz$
3. Umformen nach dx: $2*dx=dz\Longrightarrow dx={\frac {dz}{2}}$
4. Anpassung der alten Grenzen $a\longrightarrow g(a)$ $b\longrightarrow g(b)$
5. Einsetzen in das Integral: $\int _{g(a)}^{g(b)}e^{z}\,{\frac {dz}{2}}={\frac {1}{2}}*\int _{g(a)}^{g(b)}e^{z}\,dz$
6. Integration: ${\frac {1}{2}}*\int _{g(a)}^{g(b)}e^{z}\,dz={\frac {1}{2}}\left[e^{z}\right]_{g(a)}^{g(b)}$
7. Die Funktion $g(x)$ für die Variable $z$ ersetzen: ${\frac {1}{2}}\left[e^{z}\right]_{g(a)}^{g(b)}={\frac {1}{2}}\left[e^{2x}\right]_{g(a)}^{g(b)}$

Die integrierte Funktion bzw. Stammfunktion von $h(x)=e^{2x}$ lautet: $H(x)={\frac {1}{2}}*e^{2x}$

Rotationskörper (Zusatz nur für LKs*)

Rotationskörper und Raumintegrale

Lässt man den Graphen einer Funktion um die x-Achse rotieren, so entsteht ein sogenannter Rotationskörper. Für seinen Rauminhalt gilt $V_{rot}=\pi \int _{a}^{b}(f(x))^{2}dx$.

Als Beispiel betrachten wird das Volumen einer Kugel mit Radius $r$, die durch die Rotation des Graphen der Funktion $f$ mit $f(x)={\sqrt {r^{2}-x^{2}}}$ im Intervall $[-r;r]$ um die $x$-Achse entsteht. Mit der Formel für den Rotationskörper erhält man nun das Volumen der Kugel: $V=\pi \int _{-r}^{r}(r^{2}-x^{2})dx=\left[\pi (r^{2}\cdot x-{\frac {1}{3}}x^{3})\right]_{-r}^{r}={\frac {4}{3}}\pi \cdot r^{3}$

Aufgaben

Übung 1

Wie lautet die Stammfunktion dieser Funktionen?

a) $f(x)=x*sin(2x)$

Nutze die partielle Integration

Setze die leicht abzuleitende Funktion $g(x)=x$ und die leicht zu integrierende Funktion $f'(x)=sin(2x)$

$F(x)={\frac {sin(2x)}{4}}-{\frac {x*cos(2x)}{2}}+C$

b) $f(x)=x*e^{x^{2}}$

Nutze die Integration durch Substitution

Setze die innerer Funktion $g(x)=x^{2}=z$ und leite sie nach x ab

$\int x*e^{z}\,{\frac {dz}{2x}}=\int {\frac {e^{z}}{2}}\,dz={\frac {1}{2}}\int e^{z}\,dz$

$F(x)={\frac {e^{x^{2}}}{2}}+C$

c) $f(x)={\frac {e^{x}}{a-e^{x}}}$

Nutze die Integration durch Substitution

Setze die innerer Funktion $g(x)=a-e^{x}=z$ und leite sie nach x ab

$F(x)=-ln(|a-e^{x}|)+C$

Textaufgabe: Zahn-Logo für eine Praxis

Skizze des Zahn-Logos

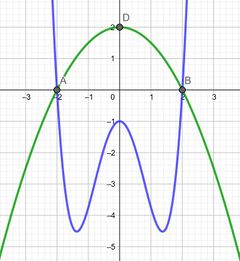
In einer Zahnarztpraxis soll ein neues Logo entworfen werden. Dazu wurde die nebenstehende Zeichnung angefertigt, welche durch die Funktionen $f(x)=-{\frac {x^{2}}{2}}+2$ und $g(x)=x^{4}-{\frac {15}{4}}*x^{2}-1$ das Zahnlogo bildet. Dabei entspricht eine Längeneinheit in dem Graphen 1 cm. Nun soll dieses Logo mit einer Dicke von 1 mm aus Silber ($1cm^{2}$ Silber wiegt 10,5 g) produziert werden. Wie schwer wird das Logo dann werden?

Zuerst muss die Fläche des Logos berechnet werden. Dazu wird dieses Integral genötigt: $\int _{-2}^{2}f(x)+g(x)\,dx$

Hast du daran gedacht, alle Einheiten einheitlich anzupassen? Die Dicke von 1 mm muss auf jeden Fall noch in cm umgerechnet werden.

Wenn du die Fläche des Logos $A_{Logo}$ wie in Tipp 1 berechnet hast, kannst du das $V_{Logo}$ nun durch das Produkt von $A_{Logo}$ und der Dicke (beachte Tipp 2!) berechnen

$A_{Logo}=3,2cm^{2}$

$V_{Logo}=A_{Logo}*Dicke_{Logo}=3,2{cm}^{2}*0,1cm=0,32{cm}^{3}$

$V_{Logo}*Gewicht_{Silber}=0,32[{cm}^{3}]*10,5[g]=3,36[g]$

Das fertige Logo aus Silber wiegt 3,36 g.

Übungsaufgabe 1: Rotationskörper und Raumintegrale

Gegeben sei die Funktion $f$ mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x) = \frac{7}{1+x}, x \in\mathbb{R}_+} . Die Fläche von f rotiere um die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} -Achse.

Berechne den Inhalt des entstehenden Drehkörpers:

a) im Intervall Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle [0; a]}

b) im Intervall Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle [0; 6]}

Nutze die Formel zur Inhaltsberechnung von Rotationskörpern Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V_{rot} = \pi \int_{a}^{b} ( f(x) )^2 dx} und setze die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} sowie die Grenzen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a} ein.

a) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V_{rot}= \pi \int_{a}^{b} ( f(x) )^2 dx = \pi \int_{0}^{a} ( \frac{7}{1+x} )^2 dx = \pi \int_{0}^{a} \frac{49}{(1+x)^2} dx = 49\pi \int_{0}^{a} (1+x)^{-2} dx = 49\pi \left[ -(1+x)^{-1} \right]_{0}^{a} = -\frac{49\pi}{1+a} + \frac{49\pi}{1} = 49\pi - \frac{49\pi}{1+a}} .

b) Für das Intervall Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle [0; 6]} gilt dann nach Aufgabenteil a): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V_{rot} = 49\pi - \frac{49\pi}{1+6} = 49\pi - 7\pi = 42\pi} .

Übungsaufgabe 2: Rotationskörper und Raumintegrale

Sei eine Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} gegeben mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x) = \frac{1}{6} x^2 + 1, x\in\mathbb{R}} sowie die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h} mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x) = -\frac{1}{3} x + 5, x\in\mathbb{R}} .

Die Graphen von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h} begrenzen mit der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y} -Achse eine Fläche.

Berechne den Inhalt des Körpers, der entsteht, wenn diese Fläche um die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} -Achse rotiert.

Überlege dir, wie die Formel aussieht, die du zur Berechnung des Inhalts zwischen zwei Funktionen nutzen musst.

Die Formel zur Inhaltsberechnung lautet: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V_{rot} = \pi \int_{0}^{b} ( h(x) )^2 dx - \pi \int_{0}^{b} ( g(x) )^2 dx } , wobei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle b} der Schnittpunkt von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)} ist. Berechne also zunächst den Schnittpunkt.

Der Schnittpunkt von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)} ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{11}{3}} . Setze dies nun als obere Grenze in deine Formel (siehe Tipp 2) ein und berechne die Integrale. Nutze dafür die Substitution sowie dein Wissen über Potenzregeln und Linearität.

1. Schnittpunkt berechnen:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x) = h(x) \Leftrightarrow \frac{1}{6} x^2 + 1 = -\frac{1}{3} x + 5 \Leftrightarrow \frac{1}{6} x^2 + \frac{1}{3} x - 4 = 0 \Leftrightarrow x^2 + 2x - 24 = 0 \Leftrightarrow x_{1,2} = -1 \pm \sqrt{1^2+24} = -1 \pm 5 \Rightarrow x_1 = 4, x_2 = -6 } Für uns interessant ist nur der Wert im positiven Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} -Bereich, da die Fläche links von der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y} -Achse laut Aufgabenstellung nicht betrachtet wird.

Setze Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x_1 = 4} in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} oder Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle g(x)} ein. Dann folgt bspw. für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(x)} : Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h(4) = -\frac{1}{3} \cdot 4 + 5 = \frac{11}{3}}

2. Integrale berechnen:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V_{rot} = \pi \int_{0}^{b} ( h(x) )^2 dx - \pi \int_{0}^{b} ( g(x) )^2 dx = V_{rot} = \pi \int_{0}^{\frac{11}{3}} ( -\frac{1}{3} x + 5 )^2 dx - \pi \int_{0}^{\frac{11}{3}} ( \frac{1}{6} x^2 + 1 )^2 dx = \pi \int_{0}^{\frac{11}{3}} ( 5 -\frac{x}{3} )^2 dx - \pi \int_{0}^{\frac{11}{3}} ( \frac{x^4}{36} + \frac{x^2}{3} + 1 ) dx}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \rightarrow} Substituiere Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle u = 5 - \frac{x}{3} \Rightarrow \frac{du}{dx} = -\frac{1}{3} \rightarrow -3\pi\int u^2 du}

Nun muss die Potenzregel angewendet und resubstitutiert werden. Im zweiten Term kann zudem die Linearität des Integrals ausgenutzt werden. Insgesamt gilt dann:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V_{rot} = \left[ \frac{(x-15)^3}{27} \right]_{0}^{\frac{11}{3}} - \left[ \frac{x^5+20x^3}{180}+x \right]_{0}^{\frac{11}{3}} \approx 58,26 }