Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Geometrie
Geometrie
Winkel
1. Winkel zeichnen und messen
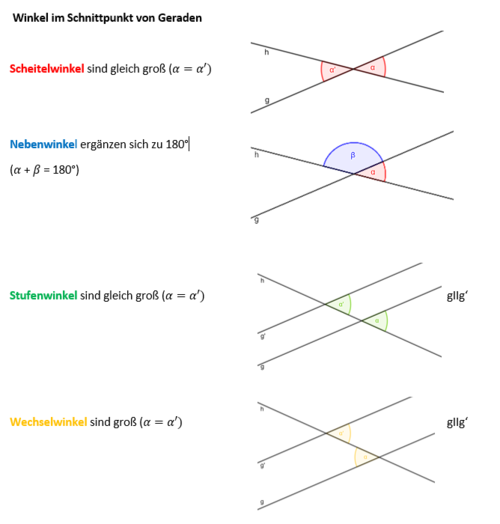
2. Winkel im Schnittpunkt von Geraden:
Dreiecke
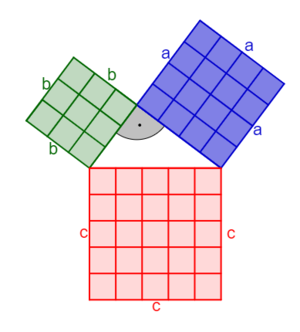
Ist das Dreieck rechtwinklig, gilt der Satz des Pythagoras und die Trigonometrie!
Satz den Pythagoras (in rechtwinkligen Dreiecken)
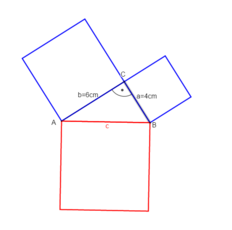
Beispiel 1: Die Katheten sind gegeben und die Hypotenuse ist gesucht.
geg: rechtwinkliges Dreieck mit γ=90°; Katheten: a = 4cm; b = 6cm
ges: Hypotenuse c
c² = a² + b² |Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \surd}
c = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sqrt{\text{a² + b²}}}
|Werte einsetzen
c = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sqrt{\text{4² + 6²}}}
|berechnen
(c = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sqrt{52}}
diesen Schritt musst du nicht notieren)
c Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \approx}
7,2 [cm]
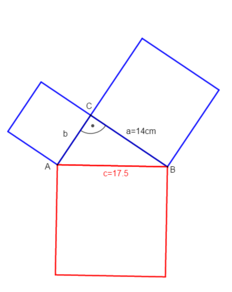
Beispiel 2: Die Hypotenuse und eine Kathete sind gegeben und die andere Kathete ist gesucht.
ges: Kathete b
a² + b² = c² |-a²
b² = c² - a² |Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \surd}
b = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sqrt{\text{c² - a²}}}
|Werte einsetzen
b = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sqrt{\text{17,5² - 14²}}}
|berechnen
(b = Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sqrt{110,25}}
diesen Schritt musst du nicht notieren)
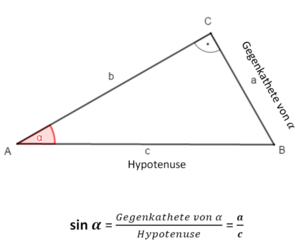
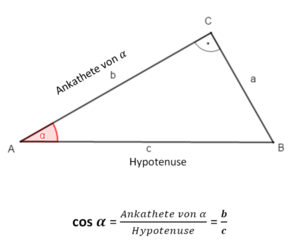
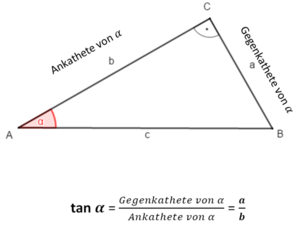
Trigonometrie (in rechtwinkligen Dreiecken)
Ebene Figuren
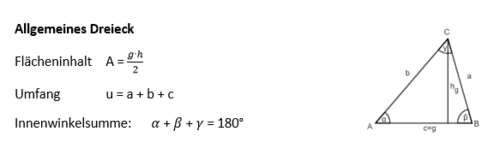
Ist das Dreieck rechtwinklig, gilt der Satz des Pythagoras und die Trigonometrie!
