Digitale Werkzeuge in der Schule/Mathematik im Beruf/Unfallforensikerinnen und Unfallforensiker

Info

In diesem Lernpfadkapitel widmen wir uns dem Beruf der Unfallforensikerinnen und Unfallforensiker.

Als Unfallforensiker oder Unfallforensikerin kann man arbeiten, wenn man eine Weiterbildung als staatlich geprüfter Techniker oder Meister oder staatlich geprüfte Technikerin oder Meisterin der Fachrichtung Kraftfahrzeugtechnik oder Maschinenbau oder vergleichbares absolviert und mindestens drei Jahre Berufserfahrung gesammelt hat. Alternativ kann man nach einem abgeschlossenen Studium, zum Beispiel im Bereich Fahrzeugelektronik, in den Beruf einsteigen. Aufgaben sind die Mitarbeit bei der Aufnahme von Verkehrsunfällen, die Sicherung technischer und digitaler Unfallspuren, Vermessung der Unfallstelle, Unfallrekonstruktionen und das Fertigen von Berichten und Stellungnahmen.

Um dieses Kapitel zu bearbeiten benötigst du das zugehörige Arbeitsblatt, Zettel und Stift, ein Geodreieck und einen Taschenrechner.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.

Am Ende dieses Kapitels kannst du:

• einen Autounfall rekonstruieren.
• ein Unfallgutachten erstellen.

Viel Erfolg!

Unfallrekonstruktion

Info

Typischerweise muss eine Unfallforensikerin oder ein Unfallforensiker vorliegende Unfallstellen vermessen, um den Unfall im Anschluss rekonstruieren zu können. Dazu ist es wichtig, dass Unfallforensikerinnen und Unfallforensiker sicher im Umgang mit Winkeln sind.

Aufgabe 1: Wiederholung zum Erkennen von Winkeln

Ordne den gezeichneten Winkeln die passende Winkelgröße zu. Überprüfe dein Ergebnis.

Achtung: Einem Winkel kann keine passende Größe zugeordnet werden.

Diese Abbildung kann dir dabei helfen, die Größen von Winkeln in Grad zu erinnern:

Merksatz zu Winkeln

Bezeichnung	Winkelbereich	Beispiel
spitzer Winkel	größer als $0^{\circ }$ und kleiner als $90^{\circ }$
rechter Winkel	$90^{\circ }$
stumpfer Winkel	größer als $90^{\circ }$ und kleiner als $180^{\circ }$
gestreckter Winkel	$180^{\circ }$
überstumpfer Winkel	größer als $180^{\circ }$ und kleiner als $360^{\circ }$

Aufgabe 2: Unfallrekonstruktion

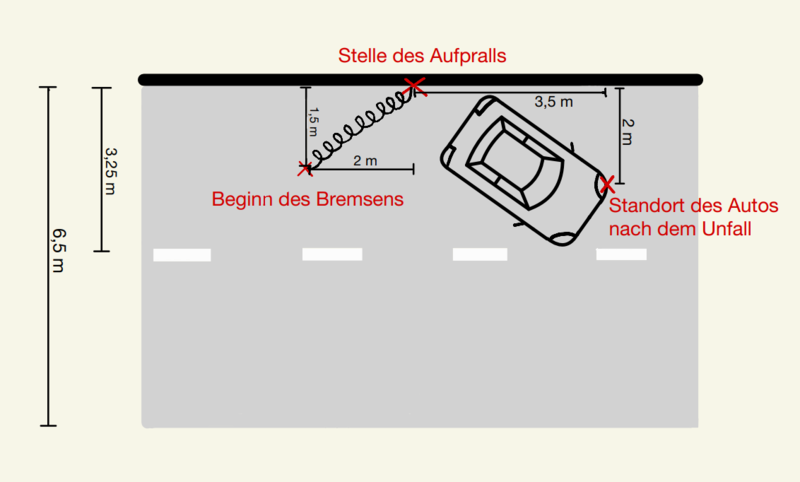
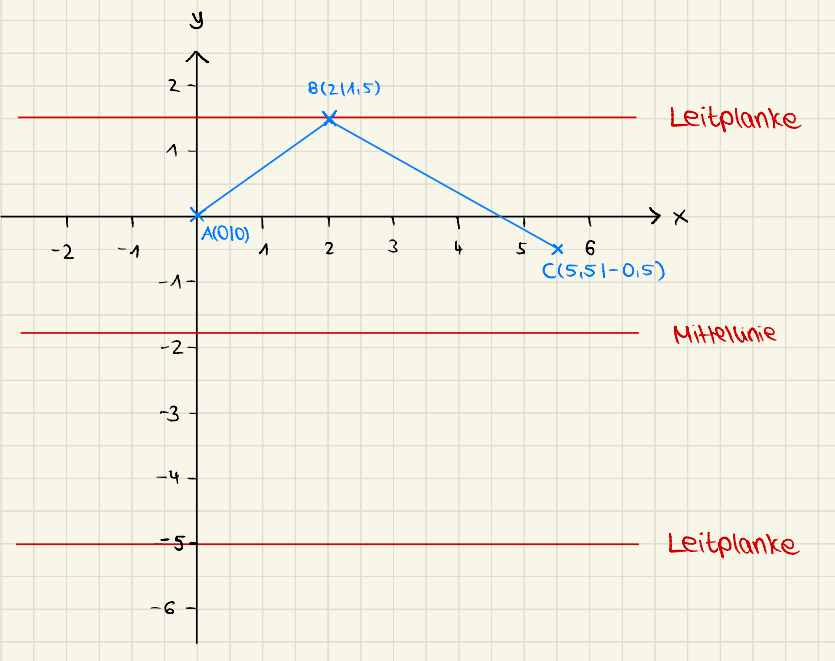
Bei einem Überholmanöver ist ein Auto mit der Leitplanke des Gegenverkehrs kollidiert. Du stellst als Unfallforensiker:in am Unfallort eine sehr kurze Bremsspur, die Stelle des Aufpralls auf die Leitplanke sowie die Position des Autos nach dem Unfall fest. Zudem nimmst du einige Messungen vor, sodass folgende Skizze des Unfallortes entsteht:

Für die Unfallrekonstruktion müssen die am Unfallort getätigten Feststellungen in eine mathematische Skizze überführt werden.

Fertige auf dem Arbeitsblatt eine maßstabsgetreue Skizze des Unfallortes in einem Koordinatensystem an.

Überlege dir für die mathematische Skizze einen geeigneten Maßstab, um den Unfall möglichst genau rekonstruieren zu können.

Falls du dir unsicher über einen geeigneten Maßstab bist, gehe davon aus, dass 2 Kästchen im Koordinatensystem $1$ m in der Realität entsprechen.

Zeichne den Beginn des Bremsens als Punkt $A(0|0)$ im Koordinatensystem ein. Überlege nun, welche weiteren Informationen aus der Skizze des Unfallortes in der mathematische Skizze zu finden sein sollten. Überlege dir ausgehend von dem Punkt $A(0|0)$, wie diese Informationen im Koordinatensystem darzustellen sind.

Betrachte die Skizze des Unfallorts und überlege anhand der angegebenen Abmessungen, wie du (1) den Beginn der Bremsspur, (2) den Aufprall des Autos sowie (3) den jetzigen Standort des Autos als drei Punkte im Koordinatensystem darstellen kannst.

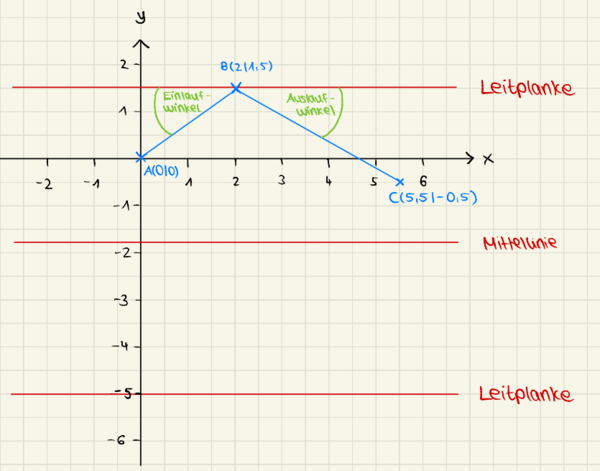
Überlege nun, wie du außerdem die Begrenzungen der Straße als Geraden im Koordinatensystem darstellen kannst.

Als Vereinfachung kannst du annehmen, dass die Bremsspur im Koordinatenursprung beginnt. Zeichne den Beginn des Bremsweges daher als Punkt $A(0|0)$ im Koordinatensystem ein. Aus den gemessenen Entfernungen in der angegebenen Skizze folgt dann, dass das Auto im Punkt $B(2|1{,}5)$ auf die Leitplanke prallte und schließlich wieder im Punkt $C(5{,}5|{-}0{,}5)$ zum Stehen kam. Zeichne diese drei Punkte in das Koordinatensystem ein. Veranschauliche nun die Begrenzungen der Straße, indem du (1) eine Gerade zeichnest, die parallel zur x-Achse auf Höhe $1{,}5$ verläuft, (2) eine Gerade als Mittellinie zeichnest, die parallel zur x-Achse auf Höhe $-1{,}75$ verläuft, und (3) eine Gerade zeichnest, die parallel zur x-Achse auf Höhe $-5$ verläuft. Zuletzt sind noch die Punkte $A$ und $B$ sowie die Punkte $B$ und $C$ jeweils zu verbinden, um den Bremsweg sowie den Weg des Autos nach Aufprall auf die Leitplanke zu veranschaulichen.

Je nachdem, welchen Maßstab du gewählt hast und welche Information der Unfallskizze du als "Ausgangspunkt" der mathematischen SKizze im Koordinatensystem gewählt hast, können sich leicht abweichende Darstellungen ergeben.

Hier wird angenommen, dass 2 Kästchen in der Realität $1$ m entsprechen. Als "Ausgangspunkt" der Skizze wurde der Beginn der Bremsspur als Punkt $A(0|0)$ festgelegt.

Aufgabe 3: Winkel messen

Info

Bei einem Verkehrsunfall bezeichnet der Einlaufwinkel den Kurswinkel eines Fahrzeugs bis hin zur Kollision. Der Auslaufwinkel hingegen meint den Kurswinkel eines Fahrzeugs unmittelbar nach der Kollision. In der folgenden Skizze kannst du erkennen, welche Winkel in der vorliegenden Unfallsituation mit dem Einlauf- und dem Auslaufwinkel gemeint sind.

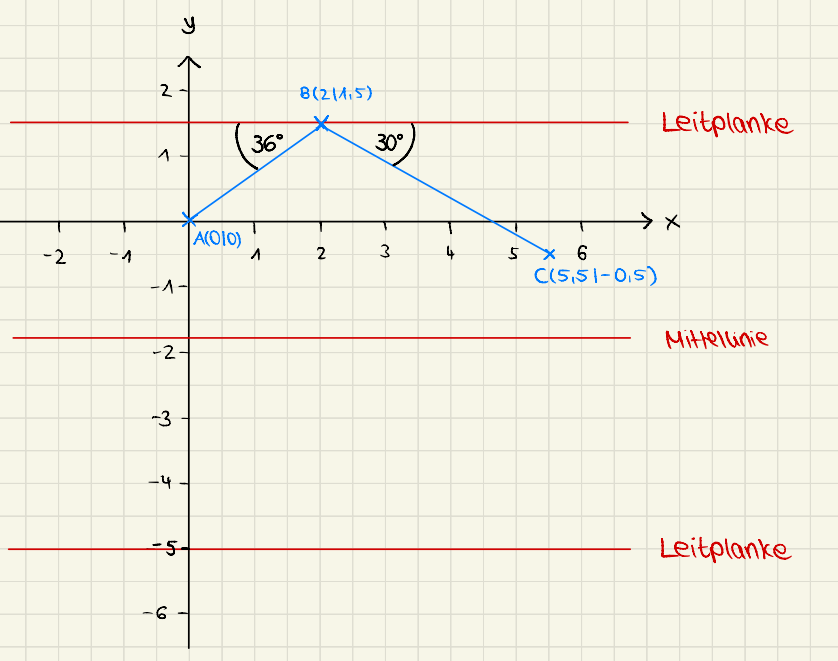
Du hast nun als Unfallforensiker:in die Aufgabe, den Einlauf- und Auslaufwinkel in der vorliegenden Unfallsituation zu bestimmen. Diese Winkel spielen bei der Schadensbegutachtung eine Rolle. Auf Grundlage der berechneten/gemessenen Winkel kann nämlich anschließend überprüft werden, welche Schäden am Fahrzeug tatsächlich durch den Unfall entstanden sein können und welche Schäden möglicherweise bereits vor dem Unfall am Fahrzeug vorlagen.

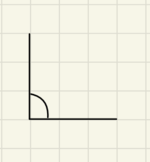
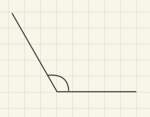
Miss daher im Koordinatensystem, das in Aufgabe 2 angefertigt wurde, den Einlauf- und den Auslaufwinkel mithilfe eines Geodreiecks. Trage die gemessenen Winkel an passender Stelle in das Koordinatensystem aus Aufgabe 2 ein.

Falls du in Aufgabe 2 keine geeignete Skizze im Koordinatensystem anfertigen konntest, mache einen Screenshot von der zur Verfügung gestellten Lösung zu Aufgabe 2. Füge dieses dann auf deinem Arbeitsblatt ein und miss dort die geforderten Winkel.

Falls du nicht mehr weißt, wie man mit dem Geodreieck Winkel misst:

Lies die Erklärung auf dieser Website nach oder schaue das Erklärvideo dort.

Nach dem Messen im Koordinatensystem ergibt sich: Einlaufwinkel $\approx 36^{\circ }$ und Auslaufwinkel $\approx 30^{\circ }$. Werden die gemessenen Winkel im Koordinatensystem aus Aufgabe 2 eingetragen, ergibt sich folgende Skizze:

Anfertigung eines Unfallgutachtens

Eine Unfallforensikerin oder ein Unfallforensiker muss Gutachten erstellen, die dann zum Beispiel an Versicherungen oder Gerichte weitergeleitet werden, um die Unfallverursacher festzustellen, Schäden zu dokumentieren und um letztendlich zu entscheiden, wer welche Kosten trägt. Daher sollst du in den folgenden Aufgaben schrittweise ein solches Gutachten erstellen.

Aufgabe 4: Berechnung zur kinetischen Energie zur Beurteilung des Schadens

Die kinetische Energie ist ein wichtiger Bestandteil des Gutachtens. Die kinetische Energie, das heißt die Bewegungsenergie, wird bei einem Unfall in Verformungsarbeit umgewandelt. Somit gilt: Je höher die kinetische Energie, desto größer sind die Schäden am Auto. So kann beispielsweise mithilfe der kinetischen Energie und durch Abgleich des realen Schadens festgestellt werden, ob das Auto zuvor schon schwerer beschädigt war. Außerdem kann eine Werkstatt daraus die Kosten für die Ausbeulung abschätzen.

Merksatz: Formel für die kinetische Energie

Die kinetische Energie bestimmt man mit der Formel $E_{\text{kin}}={\frac {m\cdot v^{2}}{2}}$, wobei die kinetische Energie Fehler beim Parsen (Konvertierungsfehler. Der Server („https://en.wikipedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle E_{\text{kin}}} in Joule [J] angegeben wird, die Masse $m$ in Kilogramm [kg] und die Geschwindigkeit $v$ in Metern pro Sekunden [${\tfrac {m}{s}}$]. Es gilt außerdem $1{\text{J}}=1{\frac {{\text{kg}}\cdot {\text{m}}^{2}}{{\text{s}}^{2}}}$.

Das Auto im Unfall aus Aufgabe 1 wiegt ca. $1{,}4$ t und ist nach kurzem Abbremsen vor dem Unfall noch Fehler beim Parsen (Konvertierungsfehler. Der Server („https://en.wikipedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle 63} ${\frac {\text{km}}{\text{h}}}$ gefahren, was durch die Betrachtung der Bremsstreifen festgestellt werden konnte.

Bestimme die kinetische Energie beim Aufprall in Joule und schreibe die Rechnung auf dem Arbeitsblatt auf. Dieser Wert wird dann an die Werkstatt weitergegeben.

Zunächst müssen alle Werte in die passenden Einheiten umgerechnet werden, damit sie in die Formel eingesetzt werden können, also in kg und ${\frac {\text{m}}{\text{s}}}$. Das sind die Einheiten, die in der Formel genutzt werden, damit bei der Rechnung das Ergebnis in Joule gegeben ist.

Überlege zuerst, wie man Tonnen in Kilogramm umrechnet, das heißt wie viele Kilogramm eine Tonne sind.

Um ${\frac {\text{km}}{\text{h}}}$ in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{\text{m}}{\text{s}}} umzurechnen, überlege, wie viele Meter ein Kilometer sind und multipliziere mit der entsprechenden Zeil. Überlege auch, wie viele Sekunden eine Stunde sind. Dabei kannst du auch einen Zwischenschritt über die Minuten machen. Dividiere dann durch diese Zahl.

Zur konkreten Berechnung: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1} t Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 1.000} kg. Um Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{\text{km}}{\text{h}}} in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{\text{m}}{\text{s}}} umzurechnen, multiplizierst du am besten erst mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1.000} , dann erhältst du einen Wert in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{\text{m}}{\text{h}}} . Dann dividierst du durch Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 3.600} bzw. zweimal durch Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 60} , denn eine Stunde sind Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 3.600} Sekunden.

Somit hat man: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1{,}4} tFehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 1.400} kg und

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{align} 63 \frac{\text{km}}{\text{h}} &= 63.000 \frac{\text{m}}{\text{h}} \\ &= 1.050 \frac{\text{m}}{\text{min}} \\ &= 17{,}5 \frac{\text{m}}{\text{s}} \end{align}}

Diese Werte kannst du dann in die Formel einsetzen.

Als erstes solltest du die Werte umrechnen: Da Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1} t Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 1.000} kg gilt, gilt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1{,}4} tFehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle = 1.400} kg. Zudem gilt:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{align} 63 \frac{\text{km}}{\text{h}} &= 63.000 \frac{\text{m}}{\text{h}} \\ &= 1.050 \frac{\text{m}}{\text{min}} \\ &= 17{,}5 \frac{\text{m}}{\text{s}} \end{align}}

Wobei im ersten Schritt durch Multiplikation mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1.000} km in m umgewandelt wurden und im zweiten und dritten Schritt jeweils durch Division durch Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 60} Stunden in Minuten bzw. Minuten in Sekunden umgewandelt wurden.

Durch Einsetzen der Werte in die Lösung ergibt sich:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{align} E_{\text{kin}} &= \frac{m \cdot v^2}{2} \\ &= \frac{1.400 \cdot 17{,}5^2}{2} \\ &= 214.375 \text{[} \frac{\text{kg} \cdot \text{m}^2}{\text{s}^2} \text{]} \\ &= 214.375 \text{[J]} \\ \end{align}}

Info

Um in Aufgabe 6 berechnen zu können, wie groß der Schaden ist, der beim Unfall auf der Oberfläche des Autos entstanden ist, hast du nun die Möglichkeit, die verschiedenen Formeln zur Berechnung des Flächeninhalts zu wiederholen.

Aufgabe 5: Wiederholung zur Berechnung von Flächeninhalten

Ordne den verschiedenen geometrischen Formen die passende Skizze sowie die geeignete Formel zur Berechnung des Flächeninhalts Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} zu. Überprüfe deine Lösung.

Technischer Benutzungshinweis

Durch Anklicken der Skizzen können diese vergrößert werden.

Aufgabe 6: Flächenberechnung des Autos

Das Auto ist durch den Unfall primär am Scheinwerfer, an der Stoßstange und durch das Schleifen entlang der Leitplanke an der Seite beschädigt.

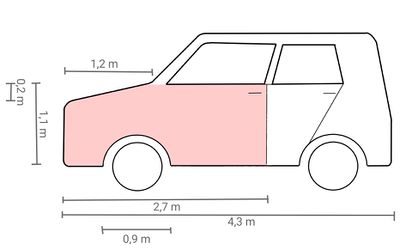
Der Scheinwerfer und die Stoßstange müssen ausgetauscht werden. Außerdem hast nach dem Unfall eine Skizze vom Auto und den beschädigten Flächen gemacht und einige Abmessungen eingetragen:

• 

Die Werkstatt benötigt die Größe dieser Fläche, um die Lackkosten und gemeinsam mit der Angabe der kinetischen Energie die Kosten für die Ausbeulung feststellen zu können.

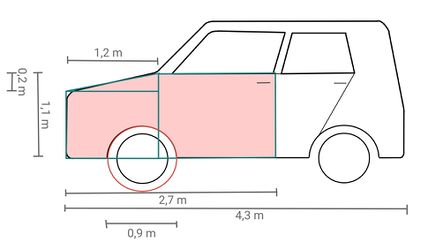
Berechne die Größe der beschädigten Autoteile in Quadratmetern. Die gesuchte Fläche ist rot markiert. Runde auf zwei Nachkommastellen und schreibe den Rechenweg auf dem Arbeitsblatt auf.

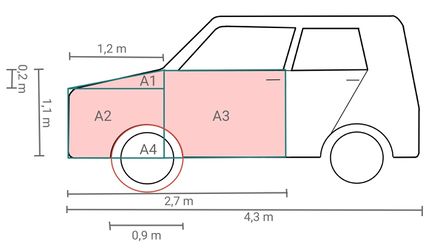
Um die Fläche ungefähr zu berechnen, kann man die Form des Autos in kleinere Flächen aufteilen und durch Kreise, Dreiecke und Rechtecke annähern. Zum Beispiel so:

• 

Anschließend werden die Teilflächen addiert (die grün umrandeten Flächen) bzw. die halbe Reifenfläche (Hälfte des rot umrundeten Kreises) wird abgezogen.

Wir berechnen mit der im Tipp gegebenen Einteilung:

• 

Dann gilt: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A1} ist ein rechtwinkliges Dreieck mit einer Höhe von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0{,}2 \text{m}} und einer Grundseite der Länge Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1{,}2 \text{m}} , somit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A1 = \frac{1{,}2 \cdot 0{,}2}{2} = 0{,}12} [m²]

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A2} ist ein Rechteck mit einer Länge von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1{,}2} m und einer Höhe von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1{,}1 \text{m}- 0{,}2 \text{m} = 0{,}9 \text{m}} , also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A2 = 1{,}2 \cdot 0{,}9 = 1{,}08 } [m²].

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A3} ist ein Rechteck mit einer Länge von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 2{,}7 \text{m} - 1{,}2 \text{m} = 1{,}5 \text{m}} und einer Höhe von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 1{,}1 \text{m}} , also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A3 = 1{,}5 \cdot 1{,}1 = 1{,}65 } [m²].

Fläche Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A4} ist ein Kreis mit Radius Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 0{,}9 \text{m}:2 = 0{,}45 \text{m}} , also Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A4 = \pi \cdot 0{,}45^2 \approx 0{,}64 } [m²].

Insgesamt ergibt sich somit für die Fläche A vom Auto: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{align} A &= A1 + A2 + A3 - \frac{A4}{2} \\ &= 0{,}12 + 1{,}08 + 1{,}65 - 0{,}32 \\ &= 2{,}53 \end{align}}

Je nachdem, wie du die Fläche angenähert hast, kann deine Lösung etwas von dieser abweichen. Nach dieser Näherungslösung ist die beschädigte Fläche ca. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 2{,}53} m² groß.

Info

Um festzustellen, ob sich eine Reparatur lohnt oder ob es sich um einen wirtschaftlichen Totalschaden handelt, werden Reparaturkosten und der Wert des Autos vor dem Unfall in Beziehung gesetzt. Um einen Totalschaden handelt es sich, wenn die Reparaturkosten die Kosten zur Wiederbeschaffung des Autos überschreiten. Dies kann gerade bei älteren Autos schnell passieren.

Wenn der Unfall allerdings nicht durch einen eigenen Fehler verursacht wurde, kann die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 130 %} -Regelung zur Anwendung kommen. Dabei gilt: Wenn die Reparaturkosten den Wiederbeschaffungswert um maximal 30 % überschreiten, also maximal 130 % betragen, muss die Versicherung des Unfallgegners die Reparaturkosten zahlen. Als Wiederbeschaffungswert wird dabei der Wert des Autos vor dem Unfall bezeichnet.

Aufgabe 7: Schadensbegutachtung

Nachdem du der Werkstatt die Schäden, auch die kinetische Energie beim Unfall sowie die Größe der beschädigten Fläche mitgeteilt hast, erfährst du, dass die Reparaturkosten für den Austausch des Scheinwerfers und der Stoßstange und die Lackierung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 4.800 \, \euro} betragen. Das Auto hat ursprünglich Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 18.000 \, \euro} gekostet. Es war vor dem Unfall allerdings schon etwa 8 Jahre zugelassen und wurde viel gefahren und hatte so vor dem Unfall bereits einen Werteverlust von ca. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 75 %} . Nun sollst du den Autofahrer oder die Autofahrerin beraten.

Bestimme den Prozentsatz der Reparaturkosten an dem Wert des Autos vor dem Unfall. Berechne dazu zunächst den Restwert des Autos vor dem Unfall (Schritt 1) und anschließend den Prozentsatz der Reperaturkosten daran (Schritt 2) und trage alle Werte in die Tabelle ein. Übertrage nach dem Überprüfen die richtigen Werte auf das Arbeitsblatt.

Entscheide, ob es sich um einen Totalschaden handelt.

Falls ja: Nimm an, dass der Unfall nicht vom Autofahrer oder der Autofahrerin selbst verursacht wurde. Entscheide, ob die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 130 %} -Regelung zur Anwendung kommen kann, ob also die Reparaturkosten den Wiederbeschaffungswert um maximal 30 % überschreiten.

Zur Berechnung des Wertes vor dem Unfall benötigst du Prozentrechnung. Dabei gilt allgemein Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle W=p \cdot G} , wobei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle W} der Prozentwert, Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle p} der Prozentsatz und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle G} der Grundwert ist. Zur Berechnung des Autowertes vor dem Unfall kannst du also die Werte (Neupreis und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 100 % - 75 % = 25 %} ) einsetzen, der Prozentsatz muss dabei geändert werden, da nicht der Wertverlust, sondern der Restwert berechnet werden soll.

Um dann den Anteil der Reparaturkosten an diesem Wert, also den Prozentsatz, auszurechnen, solltest du zusätzlich noch in einer Äquivalenzumformung die Formel umstellen.

Wir nutzen die Formel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle W = p \cdot G} .

Zu dem Restwert vor dem Unfall: Es gilt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \text{p} =25 % =0{,}25} , da der Restwert und nicht der Verlust berechnet werden soll, und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \text{G} =18.000 \, [\euro]} . Somit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \text{W} =4.500 \, [\euro]} .

Somit sind die Reparaturkosten höher als der Wiederbeschaffungswert, es handelt sich also um einen Totalschaden.

Zum Prozentsatz der Reparaturkosten am Restwert: Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \text{W} = \text{p} \cdot \text{G} \Leftrightarrow \text{p} = \frac{\text{W}}{\text{G}} \end{align}} .

Da der Prozentsatz der Reperaturkosten am Restwert bzw. dem Wiederbeschaffungswert berechnet werden soll, ist der neue Grundwert allerdings Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \text{G} =4.500} und der Prozentwert ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \text{W} =4.800} . Somit gilt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \text{p} \approx 1{,}06 =106 %} .

Also überschreiten die Reperaturkosten den Wiederbeschaffungswert um ca. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 6 %} , also kommt die Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 130 %} -Regelung zur Anwendung.

Aufgabe 8: Geschwindigkeit berechnen

Am Unfallort ist aufgefallen, dass ein zweites Fahrzeug nur knapp vor dem verunfallten Wagen zum Stehen kam. Im Rahmen der Unfallanalyse untersuchst du als Unfallforensiker:in, ob sich die fahrende Person im zweiten Auto an die vorgeschriebene Geschwindigkeitsbegrenzung gehalten hat. Um dies herauszufinden, wird die Länge der entstandenen Bremsspur gemessen. So kann mit wenigen Schritten ermittelt werden, wie hoch die Geschwindigkeit vor dem Unfall war.

Info

Die Länge des Bremsweges in Metern bei einer Gefahrenbremsung bestimmt man mit der Formel Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle b(x) = \frac{x^2}{100 \cdot 2}} , wobei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} die Geschwindigkeit in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{\text{km}}{\text{h}}} angibt.

Es ist eine Bremsspur mit einer Länge von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 32} m entstanden.

Berechne, wie hoch die Geschwindigkeit des zweiten Autos war.

Kreuze auf dem Arbeitsblatt an, ob sich die fahrende Person an die vorgeschriebene Geschwindigkeitsbegrenzung von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 50} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{\text{km}}{\text{h}}} gehalten hat.

Nutze Äquivalenzumformungen, um die Gleichung nach der gesuchten Größe Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} umzustellen! Du weißt, dass der Bremsweg Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 32} m betrug. Löse die Gleichung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 32 = \frac{x^2}{100 \cdot 2}} nach Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} auf, um die Geschwindigkeit zu bestimmen.

Multipliziere zunächst beide Seiten der Gleichung mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 200} .

Ziehe schließlich auf beiden Seiten der Gleichung die Wurzel. Entscheide, welches Ergebnis im Sachzusammenhang geeignet ist.

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{align} & & b(x) &= \frac{x^2}{100 \cdot 2} & &\mid \text{Einsetzen}\\ \Leftrightarrow & & 32 &= \frac{x^2}{200} & &\mid \cdot 200\\ \Leftrightarrow & & 32 \cdot 200 &= x^2 & &\mid \surd\\ \Leftrightarrow & & \pm \sqrt{6.400} &= x & &\mid \text{Berechnen}\\ \Leftrightarrow & & \pm 80 &= x \end{align}}

Da es keine negativen Geschwindigkeiten gibt, eignet sich im Sachzusammenhang nur die Lösung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x = 80} . Somit ist aus der Bremsspur von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 32} m auf eine Geschwindigkeit des zweiten Autos von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 80} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{\text{km}}{\text{h}}} zu schließen. Die fahrende Person hat sich also nicht an die vorgegebene Geschwindigkeitsbegrenzung von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle 50} Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{\text{km}}{\text{h}}} gehalten.

zurück zur Kapitelauswahl